Considered as one of the most interesting chapters, Coordinate Geometry is a treat for those who love to deal with the numbers. The chapter is not only a prominent part of the classes 9th and 10th syllabus but it also an important topic for various competitive exams. For all those who want to understand its meaning and concepts, we bring you a full fledged blog on Coordinate Geometry formulas!
What Is Coordinate Geometry?
Coordinate geometry is a discipline of mathematics that aids in the presentation of geometric forms on a two-dimensional plane and the learning of their properties. To get a rudimentary understanding of Coordinate geometry, we will learn about the coordinate plane and the coordinates of a point.
Understanding the Cartesian Coordinate Geometry
Before we began to explore the formulas of this chapter, let us first understand the working of coordinate geometry. In the famous Cartesian Coordinate system, there is a plane know as Cartesian plane comprises of 2 number lines which bare perpendicular to each other i.e., x- Axis (Vertical) and Y-Axis (Horizontal) which represent the two variables. The aforementioned two perpendicular lines are called the coordinate axis. Some important pointers of coordinate geometry are:
- Origin: It is the intersecting point of two lines i.e, the centre of the coordinate plane and its coordinates are (0,0)
- any random point on the coordinate plane is represented in the ordered pair of numbers. Let (c,d) is an ordered pair then, c is the x-coordinate and d is the y-coordinate
- x coordinate or Abscissa if the distance of any point from the y-axis whereas the distance of any point from x-axis is called y coordinate or ordinate
- The cartesian plane is always divided into four quadrants as I, II, III, IV
- The positive x-axis is to the right of the origin, while the negative x-axis is to the left of the origin. Also, the positive y-axis is above the origin O, while the negative y-axis is below the origin O.
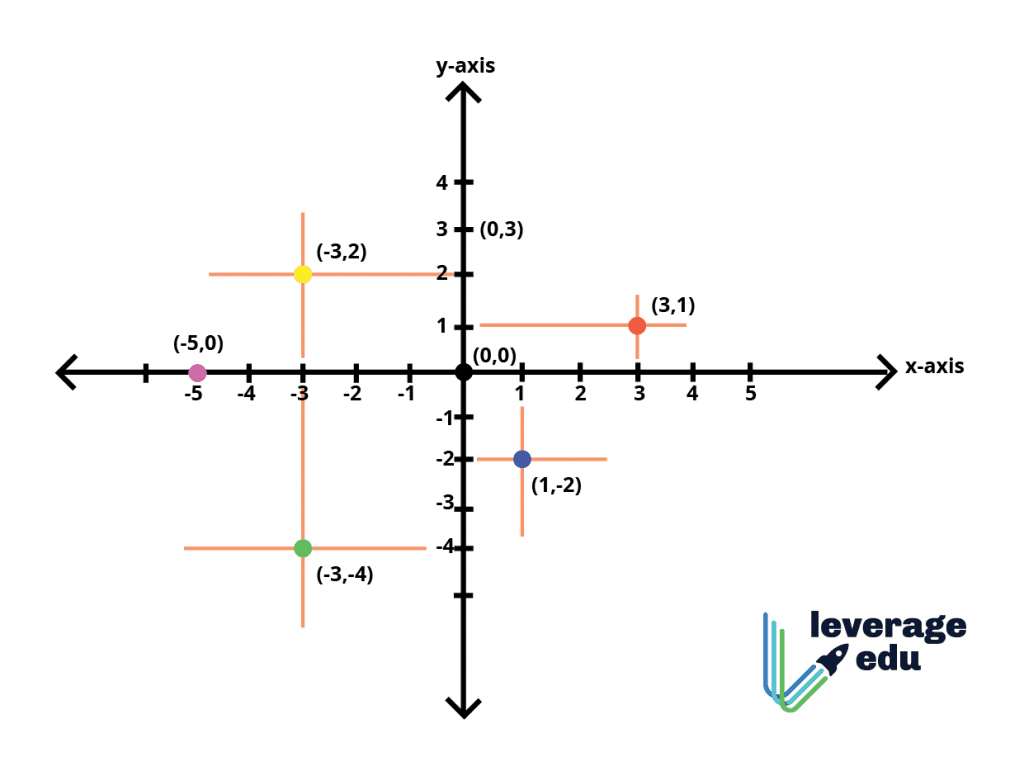
- The point represented in the first quadrant (3, 1) has both positive values and is plotted with reference to the positive x-axis and the positive y-axis.
- The point represented in the second quadrant is (-3, 2) is plotted with reference to the negative x-axis and positive y-axis.
- The point represented in the third quadrant (-3, -4) is plotted with reference to the negative x-axis and negative y-axis.
- The point represented in the fourth quadrant (1, -2) is plotted with reference to the positive x-axis and negative y-axis.
- The coordinates of a point can be used to conduct a variety of operations such as calculating distance, determining the midpoint, calculating the slope of a line, and calculating the equation of a line.
Topics in Coordinate Geometry
Before ramping on to the coordinate geometry formulas in this blog, let us first unmask some of the important topics and sub-topics that are present and are part of this branch of mathematics. The concepts and formulas required for coordinate geometry are first understood through the courses presented in coordinate geometry. The following are the topics addressed in coordinate geometry:
- The Coordinate Plane and the terms associated with it.
- Understand a point’s coordinates and how they are written in different quadrants.
- The distance between two points in the coordinate plane.
- The formula for calculating the slope of a line that connects two points.
- To get the midpoint of a line connecting two points using the Mid-point Formula.
- Section Formula for splitting the join of two points in a ratio to get the points splitting the join of two points
- Finding the centroid of a triangle with the specified three points.
- Finding the area of a triangle with three vertices.
- A line’s equation and the various forms of a line’s equation
Also Read: Top 20 Career Options in Commerce with Maths Stream
Important Coordinate Geometry Formulas
Being a one-of-a-kind chapter in class 9th and 10th Syllabus, Coordinate Geometry includes a variety of formulas which a student must learn while preparing for the exam. Learning these formulas before-hand will not only help you save time during the exam but it will also fasten your calculations. Listed below are the important coordinate geometry formulas-
- Distance of a line, PQ=
- Distance of a slope of a line= m=
= TanΘ
- Equation of a line=
or y=mx+c
- The product of the slopes of two perpendicular lines is -1
- The distance between the points (
) and (
) is PQ=
- If the point P (x,y) divides the segment AB, where A=
and B=
, internally in the ratio m:n, then,
x=
y=
- If P is the midpoint then, x=
and y=
- If G (x,y) is the centroid of triangle ABC, A=
, B=
, C=
,
then x=
and y=
- If I (x,y) is the in-centre of triangle ABC, A=
, B=
, C=
, then x=
and y=
, here a,b and c are the lengths of BC, AC and AB respectively
- y=mx+c is the equation of a straight line, where m is the slope and c is the y-intercept (tan Θ) =m, where Θ is the angle that the line makes with the positive X-axis).
- To find the coordinates of a point that divides the line segment joining points (x1,y1) and (x2,y2) in the ratio m:n, then the point (x, y) dividing these 2 points lie either on the line joining these 2 points or outside the line segment. According to the section formula, (x, y) = (mx2+nx1 / m+n , my2+ny1 / m+n)
- The area of the triangle having vertices P (x1, y1), Q (x2, y2), and R (x3, y3) is obtained from the following formula: 1/2 |x1(y2−y3) + x2(y3−y1) + x3(y1−y2)|
Find out everything about Vedic Maths in this blog!
Also Read: Class 10 Trigonometry
Coordinate Geometry – Types of Questions
Now that you are familiar with the coordinate geometry formulas, let us have a look at some pointers that we can deduce using the above-mentioned formulas when we are given coordinates of some points-
- You can calculate the distance between them
- Determine that lines formed using them are perpendicular or parallel
- Finding the slope, midpoint or equation of a line segment
- Define the equations of various geometric figures
- Calculating the area or perimeter of the figure formed through various points
Practise Questions
Now that you are through with coordinate geometry formulas and concept, here are some practice questions for you:
- Calculate the area of a triangle formed by the vertices (3,2) (6,7) and (-5,8).
- Find the coordinates of the point which will divide the line formed by joining the points (-10,7) and (8,-6) externally in ratio 3:2.
- Find the equation of the line passing through (4,6) and perpendicular to the line 6x + 2y = 8.
- Determine the slope of the line passing through A(-14,5) and B(8,-11).
- Determine the equation of the line whose slope is -3 and x intercept is 7.
- Find the coordinates of the point which will divide the line formed by joining the points (- 3,4) and (9,4) internally in ratio 5:1
- If the coordinates of one end of a diameter of a circle are(4,10) and the coordinates of its centre are (6,13), then determine the coordinates of the other end of the diameter.
- If two vertices of an equilateral triangle are (-7,4) and (-3, 12) calculate the third vertex.
Have a look at these Maths tricks that can help you solve the questions faster!
Best Books
Many times students face difficulties in understanding the difficulties in the Coordinate Geometry concepts. In that case, taking help from a reference book can help to a great extent in explaining the concepts right. Here is a list of coordinate geometry books that can help you in doing the same:
| Book Name | Link |
| The Elements of COORDINATE GEOMETRY Part-1 Cartesian Coordinatesby S L Loney | Buy Here! |
| Skills in Mathematics – Coordinate Geometry for JEE Main and Advanced 2020by Arihant Experts | Buy Here! |
| Mathematics For Joint Entrance Examination JEE ( Advanced ) Coordinate Geometryby G Tewani | Buy Here! |
| Advanced Problems in Coordinate Geometry for JEE (Main & Advanced) by Vikas Gupta | Buy Here! |
| Co-Ordinate Geometry (2-D and 3-D)by Ajay Kumar, Ravi Prakash | Buy Here! |
| The Elements of Co-Ordinate Geometry – Part 1 by S.N. Loney | Buy Here! |
| Balaji Advanced Problems in Co-Ordinate Geometry for JEE Main & Advancedby Vikas Gupta | Buy Here! |
| Eduwiser Coordinate Geometry for JEE Main and Advanced by K. C. Sinha | Buy Here! |
| Coordinate Geometry and Vectors for JEE Main and Advanced | Mathematics Module IIIby Ajay Kumar | Buy Here! |
| Fundamentals of Mathematics – Co-ordinate Geometry 2ed by Sanjay Mishra | Buy Here! |
Must Read: Statistics Formulas for GMAT Quantitative Reasoning Section
[BONUS] Here are some of our blogs on Class 9th and Class 10th Maths topics:
We hope these Coordinate Geometry formulas helped you understand the concept better! Are you struggling in making the crucial decision of stream selection after class 10th? If yes, reach out to our experts at Leverage Edu and they will provide you with the best career guidance.

 One app for all your study abroad needs
One app for all your study abroad needs





















 45,000+ students realised their study abroad dream with us. Take the first step today.
45,000+ students realised their study abroad dream with us. Take the first step today.

