Understanding Set Theory Formulas & Questions

Mathematics is known as the Queen of Sciences since ancient times and its landscape has changed considerably with more and more students choosing it as their career. It is a proven fact that the world of Mathematics has contributed a lot in producing brilliant minds and has a lucrative career to offer. The major concentrations of the subject are the structure, quantity, space as well as change. Apart from offering great academic possibilities, it is also an essential part of the competitive exams. A popular topic of the subject is Set Theory, which is a part of class 11 Maths syllabus. In this blog, you will come to know what set theory formulas are all about and what are the framed questions revolved around it. 

What is the Set Theory?

Set Theory is the process of collection of objects, sets which are known as elements or numbers. It is believed that every object in Mathematics is considered as a set and every kind of theorem is treated as predicate calculus. It has been taken by axioms of the Set Theory. Let’s understand what are the set theory formulas which are important to understand. 

The set which entails all the parts in a given collection is known as a universal set which is recognised with a ‘µ’ symbol. It is pronounced as mu. 

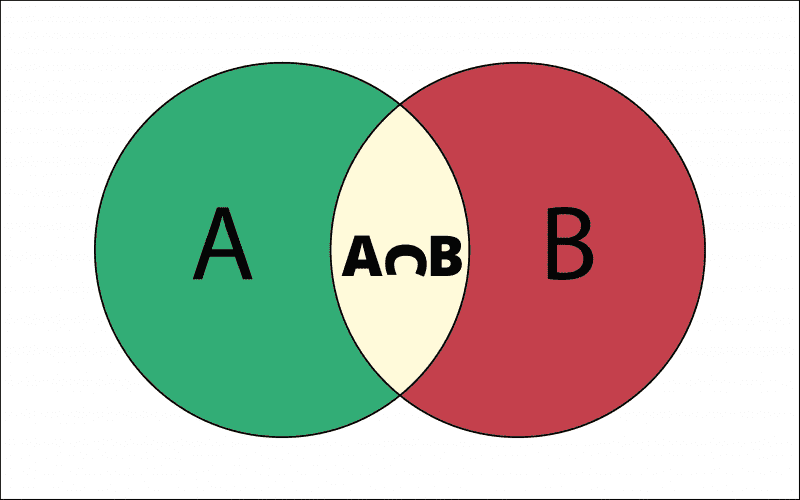
Let’s understand set A and B, the two sets. 

• The number of elements which are prevalent either in set A or B has is represented by n(AᴜB)
• n(A∩B) is the number of elements which are present in sets A and set B. 

n(AᴜB) = n(A) + (n(B) – n(A∩B)

If we talk about Set A, B & C, the formula is:

n(AᴜBᴜC) = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A∩B∩C)

Set Theory Formulas

Stated below are the important set theory formulas-

Set Theory Formulas on Properties

• Commutativity:
  • A⋂B = B⋂A 
  • A∪B = B∪A
• Associativity:
  • A⋂ (B⋂C) = (A⋂B)⋂C
  • A∪ (B∪C) = (A∪B)∪C
• Distributivity: A ⋂(B∪C) = (A ⋂B) ∪ (A⋂C)
• Idempotent Law:
  • A ⋂ A = A
  • A ∪ A = A
• Law of Ø and ∪:
  • A ⋂ Ø = Ø
  • U ⋂ A = A
  • A ∪ Ø = A
  • U ∪ A = U

Sets Theory Formulas of Difference of Sets

• A – A = Ø
• B – A = B⋂ A’
• B – A = B – (A⋂B)
• n(AUB) = n(A – B) + n(B – A) + n(A⋂B)
• n(A – B) =  n(A∪B) – n(B)
• n(A – B) = n(A) – n(A⋂B)
• (A – B) = A if A⋂B =  Ø
• (A – B) ⋂ C = (A⋂ C) – (B⋂C)
• A ΔB = (A-B) U (B- A) 
• n(A^‘) = n(∪) – n(A)

Sets Theory Formulas of Complement Sets

• Law of Double complementation: (A’)’ = A
• Laws of Empty set and Universal Set: Ø’ = ∪ and ∪’ = Ø
• Complement Law : A∪A’ = U, A⋂A’ = Ø and A’ = U –  A
• De Morgan’s Laws: (A ∪B)’ = A’ ⋂B’ and (A⋂B)’ = A’ ∪ B’

Set Theory Formula PDF

Here is a PDF for you to download the above-mentioned formulas-

Set Notation 

Before we go on and explore various types of set theory formulas, let us first understand how we can denote a set. The common way of denoting a set is listing it within curly brackets. For Example: A= {yellow, green, pink, blue, red} is a set of colours, W= {0,1, 2,3,4… 15} a set of whole numbers upto 15. 

Defining a Set 

Whilst writing a set, it is mandatory to define or explain what asset is composed of. Mentioning a proper description of the set gives a clear idea about its members. For Example: 

• B= {a, e, i, o, u} is a set containing 5 elements that are are vowels of the English alphabets 
• H= {-10…-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5…} is a set of of integers

Equal Sets  

Two given sets X and y I will only be equal if both have the exact and same number of elements. For example: X= {8, 7, 9, 10} and Y= {7, 9, 8, 10} 

Thus, X= Y 

Null Set 

An empty set for a null set is a vital concept of the set theory. If there is a set without any elements in it, we can call it a null set. An empty set is denoted by A {} or A Φ.

Union of Sets 

Union of two sets can be defined as A or B, which means that there is a new set that contains the elements that appear in set A as well as set B. For Example: 

C= {6,7,8,5,9} 

D= {5, 6,4, 3,1,2} 

C ∪ D= {1,2,3,4,5,6,7,8,9}

Intersection of Sets

You will come across a variety of questions based on intersection of sets which you will be able to solve using the set theory formulas. The intersection of two given sets is the number of elements that are common to both sets. For example: 

E= {6,7,4,5,3,1}

F= {1,2,3,4,5}

E∩ F ={1,3,4,5}

Solved Examples on Set Theory Formulas

In order to get your formulas cleared pertaining to set theories, you need to understand the questions which are very important which can give you a thorough understanding of the subject. The complete list of questions with answers is as follows:

Q1. Total of 115 people were in a group, their identity cards were examined. Some of them were processing voter ids, some had passports and some people were having both of them. The question if 65 people were having passports and about 30 people had both, how many people had voter id only and were without a passport? 

Solution:
Using Set Theory Formula: n(PᴜV) = n(P) + n(V) – n(P∩V)
115 = 65+n(V) – 30
n(V) = 80
People with only voter id are = 80-30 = 50
Answer is 50

Q2. The question of colours, let’s understand 30% of people like blue colour, 40% of people showed interest in red, 5% liked both the colours red and blue, 7% of people liked both red and green, 10% people liked green and blue. Now the question is if 86% of them liked one colour only, what %age of people had a liking of all three colours?

Solution:
Using Set Theory Formula:
n(RᴜBᴜG) = n(R) + n(B) + n(G) – n(R∩B) – n(B∩G) – n(R∩G) + n(R∩G∩B)

86 = 40+30+30-5-10-7+ n(R∩G∩B)
After Solving this the answer is 8

Q3. In a school based competition, medals were awarded in various categories. 36 medals were given to dance performers, 18 medals to music performers, 12 to dramatic performers. Say these medals were distributed to 45 people wherein 4 people only got medals in all three categories, so how many medals were received in exactly two of these categories?

Solution:
Let
A = Those who are medals in dance performance 
B =  Those who are awarded medals in dramatics
C = Those who are awarded in music genera

What is Given,

n(A) = 36
n(B) = 12
n(C) = 18
n(A ∪ B ∪C) = 45
n(A ∩ B ∩ C) = 4

Using Set Theory Formula: n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3n(A ∩ B ∩ C)
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3 × 4 ……..(i)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩C)
Therefore, n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∪ B ∪ C)

From (i) required number

= n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∪ B ∪ C) – 12
= 36 + 12 + 18 + 4 – 45 – 12
= 70 – 67 = 3
Answer is 3

Q4. Among a group of 100 people, 72 people have eligibility to speak English, 43 people can speak French language. How many can speak English language only and how many people can only speak French language and how many speak both languages?

Solution:
Let’s keep A as a group of people who speak the English language.
Let’s Keep B as the group of people who speak French language
Let’s keep A and B group of people who speak the English language but not French
Let’s keep B and A group of people who can speak French, not the English language. 

A ∩ B be the set of people who speak both French and English.

Given:

n(A) = 72
n(B) = 43
n(A ∪ B) = 100

Using Set Theory Formula: n (A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 72 + 43 – 100
= 115 – 100
= 15

Therefore, Number of persons who speak both French and English = 15

n(A) = n(A – B) + n(A ∩ B) ⇒ n(A – B) = n(A) – n(A ∩ B)
= 72 – 15
= 57

and n(B – A) = n(B) – n(A ∩ B)
= 43 – 15
= 28

Therefore, Number of people speaking English only = 57 & Number of people speaking French is 28

Q5.  Lets keep A and B a two finite sets where n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, so find n(A ∩ B).

Solution:
Using Set Theory Formula: n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Wherein n(A ∩B) = n(A) + n(B) – n(A ∪B)
= 20 + 28 – 36
= 48 – 36
= 12

Answer is 12

Q6: A survey was conducted in a class of 100 children and it was found out that 45 of them like Maths whereas only 35 like Science. 10 students like both subjects. Using set theory formula find out how many like neither of the subject?

Solution:
Total Children – 100
n(A)No. of students who like Science – 35
n(B)No. of students who like Maths – 45
n(A∩B) No. of students who like both Maths and Science – 10

Therefore using, n(AᴜB) = n(A) + (n(B) – n(A∩B) we get
35 + 45 – 10
= 70

So, the number of students who like neither of subjects is
100 – 70 = 30
Answer is 30

Also read: Algebra Formulas

Set Theory Questions with Venn Diagrams

Q1: In a survey conducted by school authorities for class X A of 30 students, it was found that 8 students like both French and English, classes. Whereas, only 18 enjoyed English. As per the school rules, it was compulsory for students to take at least one of the languages. Using set theory formula, find out how many students liked French. 

Solution: 

It is compulsory for every student to take one language, therefore we can conclude that: 
n(AᴜB) = n(µ) = 30

Moving forward with the set theory question, we know that 18 students like English whereas 8 like both English and French. Therefore, the number of students who like only English is 18- 10 = 10.

Hence, n(µ) = 30
n(E) = 10 
n(F) = 30 – 10 
= 20
Answer is 20

Set Theory Formulas and Problems

Now in order to check your mental strength, we have a list of unsolved questions which you have to solve to check your knowledge. Given below is the list of Set Theory questions curated by Leverage Edu:

Q1. Let’s Say 70% of the people like Coffee, 80% of the people like Tea. Then at least what percentage of people like both coffee and tea?

Q2. Let’s say 70% of the people like to consume Coffee, 80% of the people like to have Tea, 85% of the people like to drink Milk. Find what percentage of people like all three?

Q3. Find the equivalent sets in the following options?

(a) A = (1, 2, 3)       B = (4, 5)
(b) P = (q, s, m)       Q = (6, 9, 12)
(c) X = (x : x is a prime number less than 10)   Y = (x : x ∈ N, x ≤ 4)
(d) R = (x : x = 2n + 3, n < 4, n ∈ N}  S = {x : x = n/(n + 1), n ∈ R, n ≤ 4)
(e) The set of vowels in the English alphabet
(f) The set of consonants in the English alphabet

Q4. Let keep A = (a, b, c, d, e, f). Let’s Insert the appropriate symbol ∈ or ∉ in the blank space.

(a) d __ A
(b) y __ A
(c) m __ A
(d) a __ A
(e) e __ A
(f) x __ A

Q5. There are 35 students in art class while as in dance class we have 57 students. Let’s find the number of students who are either in art or in dance class.   

Q6. In a 40 group of class, each student plays 1 indoor game which is chess, scrabble and chess. And 18 people play chess while 20 people play scrabble and 27 play carrom. 7 people play chess and scrabble, 12 people play scrabble and carrom, 4 people play chess, carrom and scrabble. You have to find the number of students who plays 

A. Chess and carrom
B. chess, carrom but not scrabble. 

Q7. Let keep S as {1,2,3}. Write down all the possible partitions of S.

Q8. Find down the complete range of the function
f: R→wherein R defined as f(x)=sin(x).

Q9. Find the cardinality of set A and B which is explained under:
A = (a, b, c, d) and B = (1, 4, 7, 9, 10, 12, 23)

Q10. Which among the following list is not a property of a Group?

A. Commutativity
B. Associativity
C. Existence of inverse for every element
D. Existence of identity

Also read: Solve Circular Seating Arrangement Questions

This is all about set theory formulas and questions that are to be kept in mind while revising this topic of Mathematics. If you are willing to make a career in applied mathematics and computation, then let Leverage Edu be your helping hand. From selecting a suitable university to building a portfolio, candidates will get all the admission related benefits through our experts.