A conic curve has a wide range of applications in the real world. Conic curves can be seen in buildings, temples, mosques, footballs, ice-cream cones, etc. There is a specific chapter on Conic sections in class 11 which elucidates upon the applications of conic curves in various areas such as planetary motion, design of telescopes and antennas, reflectors in flashlights and automobile headlights, etc. If you are studying this chapter and need help in understanding the key pointers, here are the notes and summary on Conic sections.
This Blog Includes:
What is the Conic Section?
According to NCERT class 11 maths, a conic section is a curve made by a crossover between the surface of a cone and a plane and is commonly known as conics. There are three kinds of conics – Ellipse, Parabola, and Hyperbola. Here are the major points of difference between these three figures-
- When a cone is sliced with a plane that does not pass through the vertex, then the curves obtained are known as conic sections or conics.
- Many shapes such as parabola, hyperbola, ellipse, circle are obtained when there is intersection between a plane and a cone in different positions.
- A locus of a point that moves in a fixed plane, so that its distance from a fixed point has a ratio that is constant to its distance from a fixed straight line.
- The fixed straight line is known as a “directrix”, the fixed point is called “focus”, and the constant ratio is known as “eccentricity”.
- If the angle between the plane and the axis is above the vertex angle in a conic section, we get an Ellipse.
- When a plane is at a right angle to the axis of the conic section, the ellipse gets converted into a Circle.
- When the angle between the plane and the axis is equal to the vertex angle in a conic section, a Parabola is generated.
- A Hyperbola is created if the angle between the plane and the axis is below the vertex angle of the conic section.
Key Terms in Conic Sections
To solve the questions asked in Class 11 Conic sections, you need to learn about the terms used in various questions in the chapter. You would learn about new terms such as Eccentricity, Foci, and Directrix, length of Latus rectum, etc. Here are the major terms in this chapter:
- Focus: The point around which a conic section is shaped is called the focus.
- Eccentricity: The length between the centre and a focus is called eccentricity.
- Directrix: A directrix is a fixed-line that is used to describe a conic. There is one directrix in parabola and two in ellipses and hyperbolas.
- Latus Rectum: In Latin, ‘latus’ means side and ‘rectum’ means straight. A straight line that is parallel to the directrix of the conic and passes through its focus is called the latus rectum.
The graph of the Conic section with the equation:
Ax2 +Cy2+Dx+Ey+F=0
If A=C, it is a circle.
If AC=0, it is a parabola.
If AC>0, it is an ellipse.
If AC<0, it is a hyperbola.
Important Formulae for Class 11 Conic Sections
To identify which kind of equation is used in the conic section in class 11 maths question paper, you can use the following formula. But begin by changing the equation into this form- Ax2 +Bxy+Cy2+Dx+Ey+F=0
- If B2 -4AC < 0, and B = 0 & A = C, then it is a circle.
- If B2 -4AC < 0, and B is not equal to 0 & A is not equal to C, then it is an ellipse.
- If B2 -4AC = 0, then it is a parabola.
- If B2 -4AC > 0, then it is a hyperbola.
Class 11 Conic Sections: Circle
A collection of all the points that lie at an equal distance with respect to a stationary point in a particular plane is simply referred to as a circle. Moreover, it is also an ellipse having both the foci on a single point that is its centre. Here are the parts of the circle as mentioned in class 11 conic sections chapter:
- Center: A static point in the middle of the circle that is equidistant from its perimeter
- Radius: It is any line segment between the centre and the edge of the circle.
The equation (general) of a specific circle is evaluated as:
x2 + y2 + 2gx + 2fy + c = 0
Here, g, f and c are constants
Equation of a circle = (x – h)2 + (y – k)2 = r2, where r = radius, with center (h, k).
Example: A circle having centre is at its origin and radius is equal to 8 cm. Get the equation of the circle.
Solution:
Given- Centre is at (0, 0), radius = 8 cm.
The equation of a circle if the centre is origin:
(x – h)2 + (y – k)2 = r2 Here, h=0 and k=0
=> (x – 0)2 + (y – 0)2 = r2
=>x2 + y2 = r2
Thus, the equation of this circle would be:
x2 + y2 = 82
x2 + y2 = 64
Permutation and Combination Class 11
Class 11 Conic Sections: Parabola
As per the class 11 conic sections, we define a parabola as an accumulation of all points in a plane that lies at an equal distance from a stationary line and a stationary point (that is not on the line). The stationary line is called the directrix of the parabola, and the stationary point F is called the focus. The axis of a parabola is the line going through the focus and at a right angle to the directrix.
When we draw a parabola on a graph, the maximum or minimum value we get on the parabola is referred to as a vertex of the parabola.
Standard Equations of Parabola:
(x – h)2 = 4p (y – k), where the focus is (h, k + p) and the directrix is y = k – p
Parabola: Important Formulae
Tabulated below are the important formulae will be necessary for using questions of parabola-
| Forms of Parabola | y2 = 4ax | y2 = -4ax | x2 = 4ay | x2 = -4ay |
| Axis of Parabola | y = 0 | y = 0 | x = 0 | x = 0 |
| Directrix of Parabola | x = -a | x = a | y = -a | y = a |
| Focus | (a, 0) | (-a, 0) | (0, a) | (0, -a) |
| Length of latus rectum | 4a | 4a | 4a | 4a |
Take This Maths Quiz If You Consider Yourself Genius!
Example: Evaluate the coordinates of the focus, axis of the parabola, and the equation of directrix for the parabola for the equation, y2 = 16x.
Solution: Equation of the parabola is…
Since the coefficient of x = 16, that is positive. Thus, the parabola opens towards the right.
By comparing the given equation with y2 = 4ax,
- 4ax = 16ax
- 4a = 16
- a = 4
Coordinates of the focus: (a, 0) i.e., (4, 0)
Since the equation of parabola involves y2, the axis of the parabola is the y-axis.
Directrix of parabola is given by- x = -a
x=−3
Class 11 Conic Sections: Ellipse
Ellipse is defined as an oval-shaped figure. We can explain ellipse as a closed conic section having two foci (plural of focus), made by a point moving in such a manner that the addition of the length from two static points (two foci) does not vary at any point of time. Here are some essential points related to an ellipse that are derived from the class 11 conic sections chapter:
- Center: It is the halfway point on the specific line segment joining the two foci of the ellipse
- Major axis: It is a line segment that moves through the foci of the ellipse
- Minor axis: It is a line segment that is at a right angle to the major axis and moves across the centre of the ellipse
- Vertex: It is the endpoints of the major axis in an ellipse.
Standard Equations of an Ellipse:
x2a2+y2b2= 1, where a > b
x2a2+y2b2= 1, where a < b
Ellipse: Important Formulae
Go through the tabulated below formulae before solving questions based on ellipse-
| Forms of Ellipse | x2a2+y2b2= 1 | x2a2+y2b2= 1 |
| Equation of the major axis | y = 0 | x = 0 |
| Length of the major axis | 2a | 2a |
| Equation of minor axis | x = 0 | y = 0 |
| Length of the minor axis | 2b | 2b |
| Equation of directrix | x = ± a/e | y = ± a/e |
| Length of the latus rectum | 2b2/a | 2b2/a |
Example: Find the equation of an ellipse having the major axis along the x-axis and passing through the points (4,3) and (-1,4).
Solution:
Ellipse is of this form x2a2+y2b2=1
It passes through the points (4, 3) and (-1, 4).
We obtain these two equations (a) and (b),
16/a2+ 9/b2= 1 ………….(a)
And, 1/a2 + 16/b2 = 1…….(b)
Using substitution,
16p + 9q = 1 and p + 16q = 1, where 1/a2 = p and 1/b2 = q
By solving the equations (a) and (b) we get,
1/a2 = p = 7/247
1/b2 = q = 15/247
Thus, the equation of the ellipse will be7x2 + 15y2 = 247.
Class 11 Conic Sections: Hyperbola
Class 11 maths NCERT book states that a hyperbola is a combination of all points in a plane such that the difference between distances to two static points (foci) in a plane is constant at every point. As per the conic sections chapter of class 11, hyperbola has two stationary points that are known as the focus of the hyperbola. Have a look at the important pointer related to it-
- Center: It is the halfway point of a particular line segment connecting the two foci
- Eccentricity: The ratio between the focus (a fixed point) and the directrix (a fixed-line) of the hyperbola is called eccentricity
- Standard Equation of Hyperbola: x 2 / a 2 – y2 / b 2 = 1.
Hyperbola: Important Formulae
| Forms of hyperbola | x2a2-y2b2 = 1 | y2b2–x2a2=1 |
| Coordinates of centre | (0, 0) | (0, 0) |
| Coordinates of foci | (±ae, 0) | (0, ±ae) |
| Equation of directrix | x = ±a/e | y = ±a/e |
| Eccentricity | e=a2 + b2a2 | e=a2 + b2a2 |
| Length of the latus rectum | 2b2 /a | 2b2 /a |
| Coordinates of vertices | (±a,0) | (0, ±a) |
Example: Get the coordinates of foci, vertices, and length of the latus rectum of the following hyperbola 36x2 − 25y2 = −169.
Solution:
The equation 36x2 − 25y2 = −169 can be written as (x2 / 25) – (y2 / 36) = −1
Form of the hyperbola: (x2 / a2) – (y2 / b2) = −1
Therefore, a2 = 36, b2 = 25
⇒ a=6, b=5
The coordinates of the foci for the given equation are (0, ± be) => (0, ± 5e)
The coordinates of the vertices are (0, ± b) => (0, ± 6)
The length of latus rectum is (2a2 / b) = [2(6)2] / 4 = 36 units
MCQ
- Find an equation of the circle with centre at (0, 0) and radius r.
- x2 + y2 = r2
- x2 – y2 = r2
- x – y = r
- x2 + r2 = y2
- In an ellipse, the distance between its foci is 6 and the minor axis is 8. Then its eccentricity is
- ⅗
- ½
- ⅘
- 1/√5
- Eccentricity of ellipse x2 /a2 + y2/b2 = 1 if it passes through point (9, 5) and (12, 4) is
- √3/ 4
- √4 / 5
- √5 / 6
- √6/ 7
- The equation of the circle which passes through the point (4, 5) and has its centre at (2, 2) is
- (x – 2) + (y – 2) = 13
- (x – 2)2 + (y – 2)2 = 13
- (x)2 + (y)2 = 13
- (x – 4)2 + (y – 5)2 = 13
- The equation of the directrix of the parabola y2 + 4y + 4x + 2 = 0 is :
- x = –1
- x = 1
- x =-3/2
- x = 3/2
- The value of p such that the vertex of y = x2 + 2px +13 is 4 units above the y-axis is
- 2
- ± 4
- 5
- ± 3
- For the ellipse 3×2 + 4y2 = 12 length of the latus rectum is:
- 3
- 4
- 3/5
- 2/5
- In a parabola semi-latus rectum is the harmonic mean of the:
- segment of a chord
- A segment of the focal chord
- segment of the directrix
- none of these
- For what value of k, does the equation 9x2 + y2 = k (x2 – y2 – 2x) represent the equation of a circle?
- 1
- 2
- –1
- 4
- A conic section with eccentricity e is a parabola if:
- e = 0
- e < 1
- e > 1
- e = 1
Answers: 1, 1, 4, 2, 4, 1, 1, 4, 4
Important Questions
- Find the centre and radius of the circle (x+5)2 +(y-3)2 = 36.
- Find the equation of a circle passing through (0,0) and making intercepts a, b on the coordinate axis.
- Find the centre and radius of the circle 2x2 +2y2 -x = 0
- Find the equation of the circle with radius 5 whose centre lies on the x-axis and passes through the point (2,3).
- Find the centre and radius of the circle x2 + y2 – 8x + 10y -12 = 0.
- Find the equation of the circle passing through the points (2, 3) and (-1, 1) and whose centre is on the line x – 3y – 11 = 0.
- Find the equation of the circle with centre (1, 1) and radius √2.
- Find the equation of the circle with centre (½, ¼ ) and radius 1/12.
Does the point (-2.5, 3.5) lie on the circle, inside, or outside the circle (x2 + y2= 25).
Download the PDF for Class 11 Conic Sections
Thus, we hope that this blog helped you learned the essential concepts covered under class 11 conic sections. Confused about choosing the right course and university after 12th? Reach out to our experts at Leverage Edu and we will help you in making an informed decision towards your dream career! Sign up for an e-meeting with us today!

 One app for all your study abroad needs
One app for all your study abroad needs


















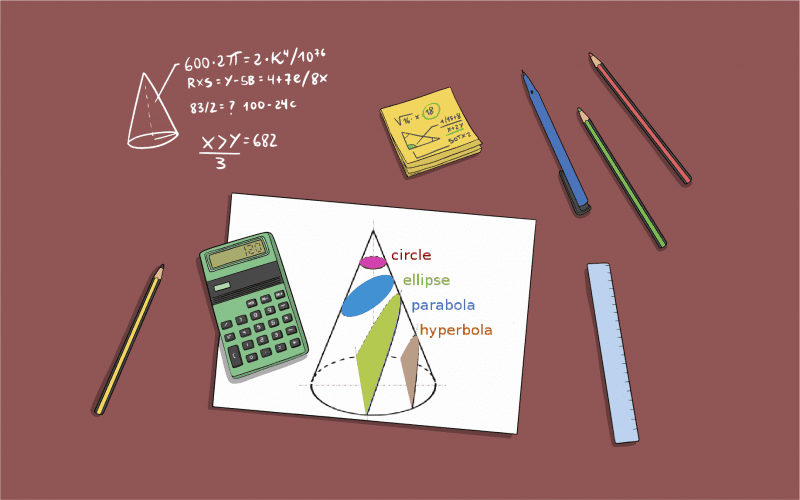


 45,000+ students realised their study abroad dream with us. Take the first step today.
45,000+ students realised their study abroad dream with us. Take the first step today.

