Class 11 Binomial Theorem

The chapters of class 11 mathematics like Binomial Theorem, Set Theory, Permutation and Combination have a significant presence in various competitive exams, especially the JEE Mains and JEE Advanced. The binomial theorem is chapter 8 of class 11 maths syllabus. Let us explore the important concepts, examples and questions that can help you in understanding the chapter better!

Binomial Theorem Identities

Here are some of the important identities which you must learn to ace this chapter-

(x+y)⁰= 1
(x+y)¹= x+y
(x+y)²= x²+2xy+y²
(x+y)³= x³+y³+3x²y+3xy²
(x+y)⁴=(x+y)³(x+y)=x⁴+4x^3‑y+4xy³+6a²b²4xy³+y⁴

The illustrative expansion depicts that

• The given term number exceeds the index by 1.For example, in the expansion of (x +y)² , term numbers are 3 whereas the index of (x +y) ² is 2
• The powers of the first quantity ‘x’ go on decreasing by 1 whereas the powers of the second quantity ‘y’ keep on increasing by 1, in the terms that follow. 
• In all the terms provided in the expansion, the addition of given indices of x and y is the equal and is called Binomial Theorem. 

Class 11 Binomial Theorem: Important Concepts 

Binomial theorem for any positive integer n, 
(x + y)ⁿ = ⁿC₀aⁿ + ⁿC₁a^n–1b + ⁿC₂a^n–2 b² + …+ ⁿC_{n – 1}a.b^n–1 + ⁿC_nbⁿ

Proof By applying mathematical induction principle the proof is obtained. 

Let the given statement be 
P(n) : (x + y)ⁿ = ⁿC₀aⁿ + ⁿC₁a^{n – 1}b + ⁿC₂a^{n – 2}b² + …+ ⁿC_n–1a.b^{n – 1} + ⁿC_nbⁿ
For n = 1, we have 
P (1) : (x + y)¹ = ¹C₀a¹ + ¹C₁b¹ = x + y Thus, P (1) is true. 
Suppose P (k) is true for some positive integer k, i.e. 
(x + y)^k = ^kC₀a^k + ^kC₁a^{k – 1}b + ^kC₂a^{k – 2}b² + …+ ^kC_kb^k … (1) We shall prove that P(k + 1) is also true, i.e., 
(x + y)^{k + 1} = ^{k + 1}C₀ a^{k + 1} + ^{k + 1}C₁ a^kb + ^{k + 1}C₂ a^{k – 1}b² + …+ ^{k + 1}C_k+1 b^{k + 1} Now, (x + y)^{k + 1} = (x + y) (x + y)^k 
= (x + y) (^kC₀ a^k + ^kC₁a^{k – 1} y + ^kC₂ a^{k – 2} b² +…+ ^kC_{k – 1} ab^{k – 1} + ^kC_k b^k) [from (1)] 
= ^kC₀ a^{k + 1} + ^kC₁ a^kb + ^kC₂a^{k – 1}b² +…+ ^kC_{k – 1} a²b^{k – 1} + ^kC_k ab^k + ^kC₀ a^kb 
+ ^kC₁a^{k – 1}b² + ^kC₂a^{k – 2}b³+…+ ^kC_k-1ab^k + ^kC_kb^{k + 1}[by actual multiplication] 
= ^kC₀a^{k + 1} + (^kC₁+ ^kC₀) a^kb + (^kC₂ + ^kC₁)a^{k – 1}b² + … 
+ (^kC_k+ ^kC_k–1) ab^k + ^kC_kb^{k + 1} [grouping like terms] = ^{k + 1}C₀a ^{k + 1} + ^{k + 1}C₁a^kb + ^{k + 1}C₂ a^{k – 1}b² +…+ ^{k + 1}C_kab^k + ^{k + 1}C_{k + 1} b^{k +1}
 (by using ^{k + 1}C₀=1, ^kC_r + ^kC_r–1 = ^{k + 1}C_r and ^kC_k = 1= ^{k + 1}C_{k + 1})

 Thus, it has been proved that P (k + 1) is true whenever P(k) is true. .According to the principle of mathematical induction, P(n) is true for every positive integer n. 

Take This Maths Quiz If You Consider Yourself Genius!

Properties of the Binomial Expansion

1. Total number of terms in the expansion of (x + a)n is (n + 1). 
2. The sum of the indices of x and a in each term is n.  
3. It is a correct expansion when the terms are complex numbers.
4. Terms that are equidistant from both ends will have coefficients that are equal. These are termed differently – binomial co-efficients.
5. General term in the expansion of (x + c)n is given by Tr + 1 = nCrx n – r ar . 
6. It is important to note that the values first increase and then decrease as you go ahead in the expansion.
7. The coefficient of xr in the expansion of (1+ x)n is nCr.

  Maths for Competitive Exams

Finding the Middle Term

Here are some simple formulas as derived from the class 11 binomial theorem chapter, that will help you understand the topic better. 

Let’s assume that we have an expression in the form (a+b)ⁿ 

And it has (n+1) terms, the middle term expansion of the (a+b)ⁿ  depends on n.

When n is even such that n=2m and is a positive integer then the total number of terms will be 2m+1. Therefore, the middle term of the expression (a+b)ⁿ  will be ½[(2m+1)+1]. Therefore, when n is even then the m+1 term and (n/2+1)th term will be the middle term.

When n is odd, such that n=2m+1 where m is a positive integer then the expansion of (a+b)ⁿ   will have a total of (m+2) terms. The middle term of the expansion of (a+b)ⁿ  will be (m+1)th and (m+2)th term or (n+1)/2 th term and (n+3)/2th term.

Important Terms on Binomial Theorem

• Binomial Expression: If an expression contains two terms combined by + or – is called a Binomial expression. For instance x+3, 2x-y etc.
• If the given expression is (a+b)ⁿ   then in its expansion the coefficient of the first term will equal to the coefficient of last term. Likewise, the coefficient of the second last term is equal to the coefficient of second term.  Hence, it is understandable that in the expansion of (a+b)ⁿ   the terms from first term and the from the last term at equal distance are having the same coefficient
• The General term:  Suppose there is an expression (a+b)ⁿ then the term(r+1)is called the general term for the expansion of the expression (a+b)ⁿ   . The general term is denoted by T_r+1 

What are Relations and Functions?

Class 11 Binomial Theorem: Solved Examples 

Now that you are through with the chapter, here are some solved examples for you to practice-

Q1. Write down the approximation of (0.99)⁵ by using the first three terms of its expansion.

We can write 99 as the sum or difference of two numbers having powers that are easier to calculate and then we can apply Binomial Theorem.
We can write it down in the form of 0.99= 1-0.01
Hence, (0.99)⁵ =(1-0.01)⁵
= C(5, 0) (-0.01) ⁰ + C(5, 1) (-0.01) ¹+ C(5, 2) (-0.01)² + ⋯
= 1 – 5(0.01) + 10(0.0001) + ⋯
≈ 1 – 0.05 + 0.001
= 0.951

Example 1: By the use of Class 11 Binomial theorem, show that–5n+6ⁿ leaves behind on dividing by 25. 

Solution:
For two numbers x and y if we can find numbers q and r such that x =yq + r, then we say that y divides x with q as quotient and r as remainder. Hence to logically explain ^– 5n+6ⁿ gets a  remainder of 1 when we divide it by 25, we are proving that– 5n+6ⁿ  = 1+25k, where k is a natural number.

Thus we get,
(1 + x)ⁿ = ⁿC₀ + ⁿC₁a + ⁿC₂a² + … + ⁿC_naⁿ For x = 5, we get 
(1 + 5)ⁿ = ⁿC₀ + ⁿC₁5 + ⁿC₂5² + … + ⁿC_n5ⁿ 
i.e. (6)ⁿ = 1 + 5n + 5².ⁿC₂ + 5³.ⁿC₃ + … + 5ⁿ 
i.e. 6ⁿ – 5n = 1+5² (ⁿC₂ + ⁿC₃5 + … + 5^n-2) 
or 6ⁿ – 5n = 1+ 25 (ⁿC₂ + 5 .ⁿC₃ + … + 5^n-2) 
or 6ⁿ – 5n = 25k+1 where k = ⁿC₂ + 5 .ⁿC₃ + … + 5^n–2

This shows that when divided by 25, 6ⁿ – 5n leaves remainder 1 

Example 2: The theorem could be illustrated through the expansion of (x + 2)⁶

Solution:
(x + 2)⁶ = ⁶C₀x⁶ + ⁶C₁x⁵.2 + ⁶C₂x⁴2² + ⁶C₃x³.2³ + ⁶C₄x².2⁴ + ⁶C₅x.2⁵ + ⁶C₆.2⁶
= x⁶ + 12x⁵ + 60x⁴ + 160x³ + 240x² + 192x + 64 

Thus (x + 2)⁶ = x⁶ + 12x⁵ + 60x⁴ + 160x³ + 240x² + 192x + 64

Class 11 Bionomial Theorem Important Questions

1. Using Binomial theorem,indicate which is larger (1.1)^10000 or 1000.
2. Find an approximation of (0.99)^5 using the first three terms of its expansion.
3. Find the expansion of (3x^2 – 2ax + 3a^2 )^3 using binomial theorem.
4. Find the value of r, If the coefficients of (r – 5)th and (2r – 1)th terms in the expansion of (1 + x)34 are equal.
5. Find x, if T11 and T12 in the expansion of (2+ x)50 are equal.Expand the expression (2x-3)6 using the binomial theorem.
6. Find the coefficient of x in the expansion of (1 – 3x + 1×2)( 1 -x)16.
7. Find the value of r, if the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x)18 are equal.
8. Evaluate (101)4 using the binomial theorem
9. Using the binomial theorem, show that 6n–5n always leaves remainder 1 when divided by 25.
10. Using Binomial theorem, expand (a + 1/b)11.
11. Write the general term in the expansion of (a2 – b )6.
12. The coefficients of three consecutive terms in the expansion of (1 + a)n are in the ratio 1:7:42. Find n.

Binomial Theorem Class 11 Miscellaneous Exercise

1. Find the coefficient of x5 in the product (1 + 2x)6 (1 – x)7 using binomial theorem.

Solution:

(1 + 2x)6 = 6C0 + 6C1 (2x) + 6C2 (2x)2 + 6C3 (2x)3 + 6C4 (2x)4 + 6C5 (2x)5 + 6C6 (2x)6
= 1 + 6 (2x) + 15 (2x)2 + 20 (2x)3 + 15 (2x)4 + 6 (2x)5 + (2x)6
= 1 + 12 x + 60×2 + 160 x3 + 240 x4 + 192 x5 + 64×6

(1 – x)7 = 7C0 – 7C1 (x) + 7C2 (x)2 – 7C3 (x)3 + 7C4 (x)4 – 7C5 (x)5 + 7C6 (x)6 – 7C7 (x)7
= 1 – 7x + 21×2 – 35×3 + 35×4 – 21×5 + 7×6 – x7

(1 + 2x)6 (1 – x)7 = (1 + 12 x + 60×2 + 160 x3 + 240 x4 + 192 x5 + 64×6) (1 – 7x + 21×2 – 35×3 + 35×4 – 21×5 + 7×6 – x7)
192 – 21 = 171

Thus, the coefficient of x5 in the expression (1+2x)6(1-x)7 is 171.

2. If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer. [Hint write an = (a – b + b)n and expand]

Solution:

In order to prove that (a – b) is a factor of (an – bn), it has to be proved that
an – bn = k (a – b) where k is some natural number.
a can be written as a = a – b + b

an = (a – b + b)n = [(a – b) + b]n
= nC0 (a – b)n + nC1 (a – b)n-1 b + …… + n C n bn
an – bn = (a – b) [(a –b)n-1 + nC1 (a – b)n-1 b + …… + n C n bn]
an – bn = (a – b) k

Where k = [(a –b)n-1 + nC1 (a – b)n-1 b + …… + n C n bn] is a natural number

This shows that (a – b) is a factor of (an – bn), where n is positive integer.

3. Find an approximation of (0.99)5 using the first three terms of its expansion.

Solution:

0.99 can be written as
0.99 = 1 – 0.01
Now by applying binomial theorem we get

(0. 99)5 = (1 – 0.01)5
= 5C0 (1)5 – 5C1 (1)4 (0.01) + 5C2 (1)3 (0.01)2
= 1 – 5 (0.01) + 10 (0.01)2

= 1 – 0.05 + 0.001
= 0.951

Class 11 Binomial Theorem PDF

Here is a PDF for this chapter-

NCERT Solutions

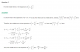
Thus, we hope that through these notes based on the class 11 binomial theorem, we have helped you in getting familiar with the chapter. For expert advice regarding which career field to opt for, reach out to our experts at Leverage Edu. Hurry Up! Book and e-meeting!