Class 9 Surface Areas and Volumes

Mathematics is enjoyable to learn and an important topic in a student’s future. Mathematics is the basis of almost all objects, such as circles, that we see or encounter around us; probability and geometry not only play a crucial role in schools, but also in real-life scenarios. A very important concept in Mathematics is Surface Areas and Volumes, which is used in our day-to-day life. this blog covers the basics of class 9 Surface Areas and Volumes for class 9.

Also Read: CBSE Class 9 Maths Syllabus

What is Surface Area?

One of the most important sub topics in class 9 Surface Areas and Volumes is Surface Area. When we calculate the space occupied by a two-dimensional object, it is called area and is measured in square units, but when we calculate the space taken up by a three-dimensional object then it is known as surface area which is also measured in square units. There are two types of surface areas –

• Total Surface Area
• Lateral/Curved Surface Area

Total Surface Area

In the chapter of class 9 Surface Areas and Volumes, it is imperative to understand the total surface area. The area which includes the base(s) as well as the curved portion, refers to the total surface area. It is the amount of the area enclosed by the object’s surface. If the object has a curved base and surface, then the sum of the two areas would be the total area.

Must Read: NCERT Solution of Maths Class 9

Lateral/Curved Area

The concept of Lateral/Curved area is also important in class 9 Surface Areas and Volumes. The area of only the curved part is known as the curved surface area or in case of cuboids or cubes, it is the area of only four sides leaving the base and top. For shapes like cylinder or cone, it is known as the lateral surface area. 

What is Volume?

The amount of space that an object or material occupies, measured in cubic units, is called volume. Two-dimensional has no volume, but just area. For example, we cannot find the volume of a circle, because it is a 2D figure, but we can calculate the volume of a sphere as it is a 3D figure.

Explore: Statistics Class 9 Maths Study Notes

Volumes and Surface Areas of Shapes

In this blog, we will learn about calculating the surface areas and volumes of the following shapes –

• Cuboid
• Cube
• Cylinder
• Cone
• Sphere

Cuboid

A Cuboid is an important part of class 9 surface area and volume. It is basically a three-dimensional figure which is made up of 6 rectangular faces, placed at right angles. Let us see what is the formula for calculating the surface area and volume of cuboid –

So, if we have a cuboid of length ‘l’, breadth ‘b’, height ‘h’, the formulae are –

• Total Surface Area

Area of face ABCD = Area of Face EFGH = (l × b) cm2
Area of face AEHD = Area of face BFGC = (b × h) cm2
Area of face ABFE = Area of face DHGC = (l × h) cm2
TSA of cuboid = Sum of areas of all 6 faces

                        = 2(l x b) +2(b x h) +2(h x l)

• Curved Surface Area

CSA = Area of face AEHD + Area of face BFGC + Area of face ABFE + Area of face DHGC
        = 2(b × h) + 2(l × h)

         = 2h (l + b) 

• Volume

Volume = l x b x h

Must Read: Class 9 Maths- Heron’s Formula

Cube

Cube is another important part of class 9 surface areas and volumes. It is basically a cuboid with further minute details. Its length, breadth and height are equal. It is made up of 6 equal squares. Let us see what is the formula for calculating the surface area and volume of cube –

So, if we have a cube with each side ‘a’, then –

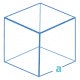
• Total Surface Area

TSA = 2(a × a + a × a + a × a)
        = 2 × (3a²) = 6a²

• Curved Surface Area

CSA = 2(a × a + a × a) 

         = 4a²

• Volume

Volume = a³

Right Circular Cylinder

Next we move on to a Right circular cylinder in class 9 Surface Areas and Volumes. A  cylinder which is circular in shape is an enclosed solid that is bound by a curved surface with two parallel circular bases. In this the two bases are precisely over each other and the axis is at right angles to the base. 

Let us consider a circular-right cylinder with height ‘h’ and radius of the base and top ‘r’ then,

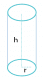
• Total Surface Area

TSA = CSA+Area of two circular bases

         = 2π x r x h + 2 x πr²

              = 2πr(h+r)

• Curved Surface Area

CSA = 2πrh

• Volume

Volume = πr²h

Must Read: Class 9 Motion Science Study Notes

Right Circular Cone

A Right Circular Cone is also an important part of class 9 Surface Areas and Volumes. A circular right cone is a circular cone whose axis is perpendicular to the base thereof. Before getting into the surface area and volume, we need to understand the relation between height and slant height.

A right cone which is circular in shape has ‘h’ height and has a perpendicular height, a slant height ‘l’ and radius of the circular base ‘r’, then

 l² = h² + r²

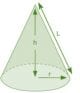
• Total Surface Area

TSA = CSA + area of base

        = πrl + πr²

        = πr(l+r)

• Curved Surface Area

CSA = ½ x 2πr x l

         = πrl

• Volume

Volume = 1/3πr²h

Also Read: Matter in our Surroundings Class 9 Notes

Sphere

We further move on to a sphere in class 9 Surface Areas and Volumes. A sphere in simple words is a closed three-dimensional solid figure. All the points on the sphere’s surface are equidistant from the “centre” common fixed point. “The “radius” is called equidistant.

So, we if have a sphere with a radius ‘r’ then,

• Total Surface Area

Incase of a sphere, TSA = CSA; TSA = 4πr²

• Volume

Volume = 4/3πr³

Overview of all formulas

Shape	TSA	CSA	Volume
Cuboid	2(lb+bh+lh)	2h(l+b)	l x b x h
Cube	6a2	4a2	a3
Right circular cylinder	2πr (h + r)	2πrh	πr2h
Right circular cone	πr(l+r)	πrl	1/3πr2h
Sphere	4πr2	–	4/3πr3

Practice Questions of Class 9 Surface Area and Volume

1. Two equal halves are made of a spherical ball. If we know that the curved surface area of each half of the ball is 56.57 cm, will you be able to deduct the volume of the spherical ball?
2. A piece of canvas was given to Meera as a gift, whose area is 551 m². Meera decides to use it to have a conical tent made, the base radius of which will be 7 m. Assuming that all the stitching margins and the wastage incurred while cutting, amounts to approximately 1 m², find the volume of the tent that can be made with it.
3. Ashita has a cube for a toy. The surface area of the cube in totality is 726 cm². You have to decipher the length of the edge of the cube. 
4. If a beautiful carved wooden box with intricate designs is made up of dimensions 8 m x 7 m x 6 m and it is to carry several other boxes of dimensions 8 cm x 7 cm x 6 cm, can you decipher the maximum number of boxes the beautiful carved wooden box can carry?  
5. Calculate and find the area of a sheet which is required to further make a closed cylindrical vessel. The height of the closed cylindrical vessel should be 1 m and diameter 140 cm.
6. A cone which was 8.4 cm high in its height and the radius of its base was 2.1 cm was melted and recast into a sphere. Find the radius of the sphere.
7. The radius of a spherical red balloon with beautiful designs increases from 6 cm to 12 cm when air is pumped into it. Can you calculate what will be the ratio of surface areas of the original balloon as compared to the new balloon as a result of the pumping of air?
8. If the heights of two cylinders are in the ratio of 4: 3 and their radii are in the ratio of 3: 4 then what is the ratio of their volumes?
9.  If a right circular cone has a radius of 4 cm and slant height 5 cm then what is its volume?
10.  A bright red brick measures 30 cm × 10 cm ×  How many more bricks will be required for a wall 30 m long. 2 m high and  thick?

Explore: Class 9 Social Science -Democratic Rights Notes

We hope that this blog has helped you understand the basics of Surface Areas and Volumes. If you want to learn more or want an insight into various subjects such as Class 9 Chemistry, Biology, English, Physics, please refer to our extensive study notes. For any career-related guidance, contact the experts at Leverage Edu and take a step forward on your path to excellence.