Class 11 Straight Lines

The chapter 10 Straight Lines will be your dose for mathematical geometry as per class 11 maths syllabus. As geometry has been an integral part of the curriculum since junior classes, the same is even followed in class 11th and 12th. You must have been through the graphical representation of equations via chapters like linear equation in one variable. Thus, class 11 straight lines chapter will equip you with advanced knowledge of this concept. So let’s go through our notes and understand the chapter. 

[powerkit_toc title=”This Blog Includes:”]

What is a Straight Line?

Any line that can be traced by a point travelling in a direction with zero curvature is known as a straight line. A straight line extends in two directions forever while having only one dimension and length. It is an important concept of geometry that is useful in various ways.

Slope of a Line

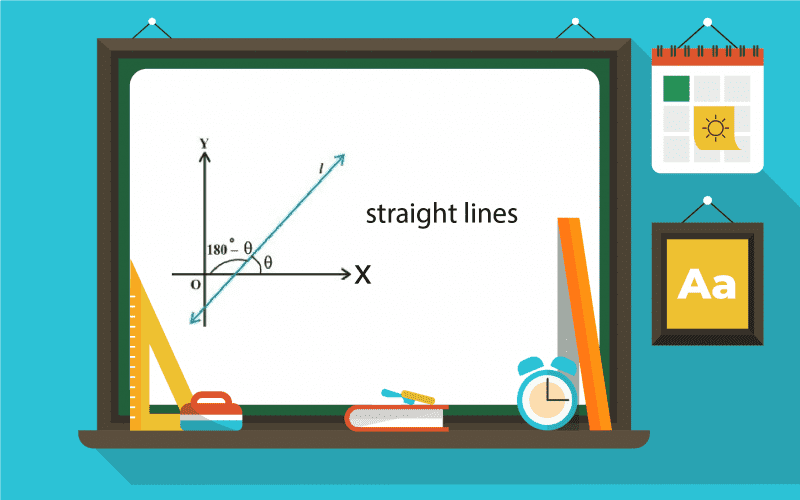
To represent a line algebraically, the slope is an essential part because, in a coordinate plane, it forms two angles with the x-axis in supplementary form. As per class 11 straight lines chapter, the slope of a line can be determined with the value of tan θ. Wherein, within the positive direction of the line in an anti-clock direction, an angle is made by θ. 

If the slope of the line passes through two points, i.e., P (a1, b1) and Q (a1, b2), then it becomes: m = tan θ = b2-b1/a2-a1.

Let us understand this through an example, let P (a1, b1) and Q (a1, b2) be any two points on a non-vertical line. The inclination of these lines will be θ, and it will be acute or obtuse. Under both the scenarios, the slope of the line will pass through point P and Q only.

Take This Maths Quiz If You Consider Yourself Genius!

Various Forms of the Equation of a Line

Class 11 maths NCERT states that every line in a plane has infinitely many points. By using the relationship between the line and points, several equations can be solved. Below mentioned are different conditions that explain the equations of a line. 

Horizontal and Vertical Lines

Derived form class 11 straight lines under this condition, if a horizontal line is distanced from a point to the x-axis, then every point will ordinate either positive or negative respectively, i.e., +a or -a. Similarly, it will be same for the vertical line also, but from a different axis than x-axis, i.e., y-axis.

Point-Slope Form
Let P0 (x0, y0) be a fixed point on a non-vertical line with assumed slope “m”. If P (x, y) is an arbitrary point on the non-vertical line then, the point (x, y) will lie with slope “m” on the same line through the fixed point (x0, y0) with equation y – y0 = m (x – x0).

Two-Point Form
If an imaginary line “L” passes through any two given points, i.e. P1 (x1, y1) and P2 (x2, y2) then, with general point P (x, y), all the three points, i.e. P1, P2, and P3 will be collinear, and the equation will be y−y1 = y2−y1 / x2−x1 * (x−x1).

Slope-Intercept Form
Let us assume that a line cuts the slope from the y-axis at a distance “c”, then the distance “c” will be called a y-intercept of the line. When the line meets the y-axis, the coordinates will be (0, c) and the equation will be y = mx + c wherein the “c” can be positive or negative as mentioned in class 11 straight lines. If the line makes an x-intercept of the line instead of the y-intercept of the line, then the equation will be y = m (x-d).

Intercept-Form
If a line makes “x-intercept a” and “y-intercept b” on any axis and the line meets x-axis at point (a, 0) and y-axis at point (0, b), then the equation according to two forms will be x/a + y/b = 1.Go through the class 11 maths NCERT solutions and get a good grip over the topic.

General Equation of a Line

A general equation of first degree in two variables will always be Ax + By + C = 0. Wherein A, B, and C will be real constants with A and B a non-zero value. Graph of such an equation will always be a straight line, and therefore the equation Ax + By + C = 0 is called a general linear equation or general equation of a line. According to class 11 straight lines chapter, the general equation can be reduced into several other forms of equations by using the slope-intercept form, intercept form, and normal form.

Slope-Intercept Form

If B is not equals to 0, then the equation Ax + By + C = 0 can be rewritten as y = mx + c. If B equals to zero, then x = -c/a.

Intercept Form

If C is not equals to 0, then the equation Ax + By + C = 0 can be rewritten as x/a + y/b = 1. If C equals to 0, then the equation Ax + By + C = 0 can be rewritten as Ax + By = 0.

Distance between Two Parallel Lines

The slopes of two parallel lines will always be equal is one of the most essential concepts that are mentioned in class 11 straight lines chapter. If we take two parallel lines in the form of y = mx + c1 and y = mc + c2, then the distance between the two lines will be equal to the length of the perpendicular. The equation for the two lines can be written as Ax + By + C1 = 0 and Ax + By + C2 = 0.

Let us have a look at solved example-

Q: If points (x, 1), (2, 1), and (4, 5) are collinear, then find the value of x.

Solution: The slope of AB = Slope of BC
(1+1) / (2-x) = (5-1) / (4-2)
2 / (2-x) = 2
2 = 2 * (2-x)
2 = 4 – 2x
2x = 2
x = 2 / 2
x = 1

Straight Lines: Practice Questions

Here are some practices questions based on the similar concepts as mentioned in class 11 straight lines chapter.

1. In the given equation 2x + y – 3 =0, 5x + ky – 3 = 0 and 3x – y – 2 = 0, if all the three lines are concurrent, then find the value of k.
2. If a line is passing through the point (2, 3) with an angle of 60° from the x-axis, then find the equation of the line.
3. What will be the distance of a point from a line?
4. Find the distance between parallel lines 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0.
5. How coordinated geometry and analytical geometry are related to each other?
6. Find the measure of the angle in between the lines x+y+7=0 and x-y+1=0.
7. Find the equation of the line, which makes intercepts -3 and 2 on the x and y-axis respectively.
8. Find the points on the x-axis whose distance from the line equation (x/3) + (y/4) = 1 is given as 4units. 
9. At what point is the origin shifted, if the coordinates of the point (,5)become (3,7)?
10.  Find the intercepts cut off by the line 2a-b+16=0
11.  Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
12.  Determine x so that the inclination of the line containing the points (x,-3) and (2,5) is 135.
13.  Find the equation of the line which passes through the point (3,4) and the sum of whose intercepts on the axes is 14. 
14.  Using slopes, find the value of x for which the points (x,-1) (2,1) and (4,5) are collinear.
15.  Find the value of K, given that the distance of the point (4,1) from the line 3x-4y+k=0 IS 4 units.

Thus, we hope that through this blog that aims to explain the core fundamentals of class 11 straight lines with informative examples, you have understood the chapter in an easy to understand way. If you are clueless about how to proceed in the right direction leading towards your career goals, reach out to our career experts at Leverage Edu and they will guide you the best. Book an e-meeting now!