Height and Distance questions are an important part of the quantitative aptitude section in various competitive exams. These types of questions are covered to test the mathematical and analytical skills of a candidate. These questions are also to assess the geometric understanding and spatial reasoning of a candidate. Height and Distance Problems are asked in exams like CAT, GATE, UPSC, and more.
Start your preparation by solving these questions. In this blog, we will go over the fundamentals of Height and Distance problems, as well as the types of questions asked in previous year exams and how to approach them. This will help you clear your basics and answer these Height and Distance questions.
Table of Contents
What is Height and Distance? What are Height and Distance Problems?
Height is the measurement of a particular object in the vertical direction. Whereas, distance is the measurement of an object from a specific point in the horizontal direction. Height and distance problems typically involve finding the height or distance of an object or point based on given information and geometric principles. Solving these types of questions involves knowledge of strong trigonometric principles.
Height and Distance Formulas:
In this section, you can see different cases while solving the height and distance questions.
Case 1: If the problem in the question focuses on the height of a tower, the distance of an object from the foot of the tower, a building or hill, the angle of elevation, etc., then the given diagram along with the formulas will help.
In right triangle ABC,
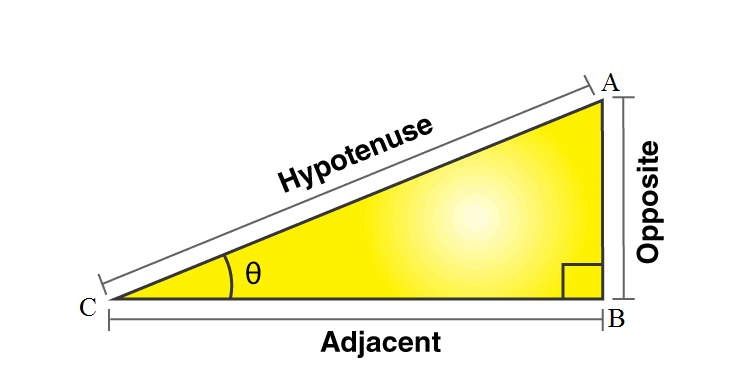
sin θ = Opposite/Hypotenuse = AB/AC
cos θ = Adjacent/Hypotenuse = BC/AC
tan θ = Opposite/Adjacent = AB/BC
Case 2: In this case, the commonly solved problems revolve around the movement of an observer. If the observer is moving toward objects like a tower, building, hill, etc., then the angle of elevation increases. The angle of elevation decreases when the observer moves away from the object. In this case, you can use the given formula to find out the distance.
In right triangle given below, d is the distance between C and D.

d = h(cot x – cot y)
Case 3: There can be another case where you can get similar triangles with the same angle of elevation or angle of depression. These questions can be solved with the help of the given formulas.
In right triangle ABC, DE || AB,

Here, triangles ABC and EDC are similar.
Using Thales or BPT theorem we can write the ratio of sides as:
AB/ED = BC/DC
50+ Height and Distance Questions and Answers For Practice
a) 15 meters
b) 10.6 meters
c) 21.2 meters
d) 30 meters
Answer: a) 15 meters
a) 15 meters
b) 30 meters
c) 60 meters
d) 45 meters
Answer: b) 30 meters
a) 5 meters
b) 10 meters
c) 13 meters
d) 15 meters
Answer: a) 5 meters
a) 15 meters
b) 30 meters
c) 10 meters
d) 20 meters
Answer: c) 10 meters
a) 4√3 meters
b) 4 meters
c) 8 meters
d) 4√2 meters
Answer: a) 4√3 meters
a) 50 meters
b) 86.6 meters
c) 100 meters
d) 75 meters
Answer: b) 86.6 meters
a) 100 meters
b) 150 meters
c) 200 meters
d) 250 meters
Answer: c) 200 meters
a) 12 meters
b) 18 meters
c) 14 meters
d) 15 meters
Answer: a) 12 meters
a) 25 meters
b) 50 meters
c) 100 meters
d) 75 meters
Answer: b) 50 meters
a) 7.5 meters
b) 10 meters
c) 15 meters
d) 20 meters
Answer: a) 7.5 meters
a) 20 meters
b) 30 meters
c) 40 meters
d) 50 meters
Answer: b) 30 meters
a) 8660 meters
b) 5000 meters
c) 7500 meters
d) 4330 meters
Answer: a) 8660 meters
a) 15 meters
b) 30 meters
c) 25.98 meters
d) 25 meters
Answer: c) 25.98 meters
a) 100 meters
b) 141.42 meters
c) 200 meters
d) 70.71 meters
Answer: b) 141.42 meters
a) 25 meters
b) 50 meters
c) 100 meters
d) 75 meters
Answer: a) 25 meters
a) 12 meters
b) 16.97 meters
c) 20 meters
d) 15 meters
Answer: b) 16.97 meters
a) 20 meters
b) 40 meters
c) 34.64 meters
d) 17.32 meters
Answer: c) 34.64 meters
a) 25 meters
b) 50 meters
c) 43.3 meters
d) 20 meters
Answer: c) 43.3 meters
a) 15 meters
b) 30 meters
c) 60 meters
d) 20 meters
Answer: b) 30 meters
a) 25 meters
b) 35.36 meters
c) 50 meters
d) 17.68 meters
Answer: b) 35.36 meters
a) 13.54 meters
b) 50 meters
c) 57.74 meters
d) 132.69 meters
Answer: c) 57.74 meters
What is the angle of elevation of the sun when a 30-meter high pole casts a shadow of 20 meters?
A) 30 degrees
B) 45 degrees
C) 60 degrees
D) 75 degrees
Answer: B) 45 degrees
A ladder is 10 meters long and makes an angle of 60 degrees with the ground. How high does the ladder reach on the wall?
A) 5 meters
B) 7.5 meters
C) 8.66 meters
D) 10 meters
Answer: C) 8.66 meters
If the angle of elevation of a tower from a point is 45 degrees and the distance from the point to the tower is 50 meters, what is the height of the tower?
A) 35.36 meters
B) 50 meters
C) 70.71 meters
D) 100 meters
Answer: C) 70.71 meters
A man is standing on the top of a 50-meter high building. He observes a car at an angle of depression of 30 degrees. What is the distance between the car and the building?
A) 25 meters
B) 50 meters
C) 86.6 meters
D) 100 meters
Answer: C) 86.6 meters
If the angle of elevation of a cloud from a point 60 meters above a lake is 30 degrees, find the distance of the cloud from the point.
A) 60 meters
B) 120 meters
C) 173.2 meters
D) 346.4 meters
Answer: C) 173.2 meters
A tree casts a shadow 24 meters long when the angle of elevation of the sun is 45 degrees. What is the height of the tree?
A) 12 meters
B) 16 meters
C) 24 meters
D) 48 meters
Answer: C) 24 meters
A tower stands vertically on the ground. From a point on the ground, the angle of elevation of the top of the tower is 60 degrees and from another point 10 meters away from the first point, the angle of elevation of the top of the tower is 30 degrees. Find the height of the tower.
A) 10 meters
B) 20 meters
C) 30 meters
D) 40 meters
Answer: B) 20 meters
A kite is flying at a height of 60 meters. The length of the string is 100 meters. What is the angle of elevation of the kite?
A) 30 degrees
B) 45 degrees
C) 60 degrees
D) 75 degrees
Answer: A) 30 degrees
A man observes a bird on the top of a tree with an angle of elevation of 30 degrees. If the man is 10 meters away from the tree, what is the height of the tree?
A) 5 meters
B) 10 meters
C) 17.32 meters
D) 20 meters
Answer: C) 17.32 meters
A vertical pole of height 15 meters casts a shadow 12 meters long on the ground. What is the angle of elevation of the sun?
A) 45 degrees
B) 50 degrees
C) 60 degrees
D) 75 degrees
Answer: A) 45 degrees
A person standing 20 meters away from a tower observes the angle of elevation of the top of the tower as 30 degrees. What is the height of the tower?
A) 10 meters
B) 15 meters
C) 20 meters
D) 30 meters
Answer: B) 15 meters
If a pole of height 6 meters casts a shadow 4 meters long, what is the angle of elevation of the sun?
A) 30 degrees
B) 45 degrees
C) 60 degrees
D) 75 degrees
Answer: B) 45 degrees
A ladder is placed against a wall. If the ladder is 10 meters long and the foot of the ladder is 6 meters away from the wall, how high up the wall does the ladder reach?
A) 6 meters
B) 8 meters
C) 9.8 meters
D) 10 meters
Answer: C) 9.8 meters
A kite is flying at an angle of elevation of 60 degrees. If the kite’s string is 100 meters long, how high isthe kite above the ground?
A) 50 meters
B) 86.6 meters
C) 100 meters
D) 173.2 meters
Answer: C) 100 meters
The angle of elevation of the top of a tower from a point 30 meters away from its base is 45 degrees. What is the height of the tower?
A) 30 meters
B) 30√2 meters
C) 45 meters
D) 45√2 meters
Answer: B) 30√2 meters
A person standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60 degrees. If the width of the river is 50 meters, how far is the tree from the person?
A) 25 meters
B) 50 meters
C) 50√3 meters
D) 100 meters
Answer: C) 50√3 meters
A man on a cliff observes a boat at an angle of depression of 30 degrees, which is sailing directly towards the cliff. If the boat is 100 meters away from the cliff and the cliff is 50 meters high, how far has the boat sailed from its initial position?
A) 25 meters
B) 50 meters
C) 75 meters
D) 100 meters
Answer: B) 50 meters
A man observes the angle of elevation of a kite as 60 degrees. If the kite’s string is 100 meters long, how high is the kite above the ground?
A) 50 meters
B) 86.6 meters
C) 100 meters
D) 173.2 meters
Answer: A) 50 meters
A vertical pole of height 20 meters casts a shadow 15 meters long on the ground. What is the angle of elevation of the sun?
A) 37 degrees
B) 45 degrees
C) 53 degrees
D) 60 degrees
Answer: A) 37 degrees
The angle of elevation of the top of a tower from a point 40 meters away from its base is 30 degrees. What is the height of the tower?
A) 20 meters
B) 20√3 meters
C) 30 meters
D) 30√3 meters
Answer: D) 30√3 meters
A man standing 15 meters away from a lamppost observes that the angle of elevation of the top of the lamppost is 30 degrees. What is the height of the lamppost?
A) 7.5 meters
B) 15 meters
C) 30 meters
D) 30√3 meters
Answer: A) 7.5 meters
A ladder 15 meters long leans against a wall forming an angle of 60 degrees with the ground. How high up the wall does the ladder reach?
A) 7.5 meters
B) 15 meters
C) 15√3 meters
D) 30 meters
Answer: B) 15 meters
The angle of elevation of the top of a tower from a point 50 meters away from its base is 60 degrees. What is the height of the tower?
A) 25 meters
B) 25√3 meters
C) 50 meters
D) 50√3 meters
Answer: B) 25√3 meters
A man standing 30 meters away from a lamppost observes that the angle of elevation of the top of the lamppost is 45 degrees. What is the height of the lamppost?
A) 15 meters
B) 30 meters
C) 30√2 meters
D) 45 meters
Answer: C) 30√2 meters
A 20-meter high tower casts a shadow 30 meters long. What is the angle of elevation of the sun?
A) 37 degrees
B) 45 degrees
C) 53 degrees
D) 60 degrees
Answer: A) 37 degrees
A man observes the angle of elevation of a cliff as 45 degrees. If he is standing 20 meters away from the base of the cliff, what is the height of the cliff?
A) 10 meters
B) 20 meters
C) 20√2 meters
D) 30 meters
Answer: C) 20√2 meters
The angle of elevation of the top of a tower from a point 25 meters away from its base is 30 degrees. What is the height of the tower?
A) 12.5 meters
B) 25 meters
C) 25√3 meters
D) 50 meters
Answer: B) 25 meters
A man observes the angle of elevation of a mountain as 60 degrees. If he is standing 100 meters away from the base of the mountain, what is the height of the mountain?
A) 50 meters
B) 100 meters
C) 100√3 meters
D) 200 meters
Answer: C) 100√3 meters
A man observes the angle of elevation of the top of a tree as 30 degrees. If he is standing 20 meters away from the base of the tree, what is the height of the tree?
A) 10 meters
B) 20 meters
C) 20√3 meters
D) 30 meters
Answer: B) 20 meters
The angle of elevation of the top of a tower from a point 40 meters away from its base is 45 degrees. What is the height of the tower?
A) 20 meters
B) 40 meters
C) 40√2 meters
D) 60 meters
Answer: C) 40√2 meters
Also Read: Questions of Syllogism Reasoning | Verbal Reasoning
Tips to Solve Height and Distance Questions
Following are some tips to solve Height and Distance questions-
- Understand the problem first and then figure out the formula that will fit into the scenario.
- Practice multiple questions to solve the problems easily and quickly.
- Draw and visualize the problem to understand it better.
FAQs
These questions assess geometric understanding and spatial reasoning skills, crucial for various professions requiring problem-solving abilities.
Basic geometry, trigonometry, and spatial reasoning are key. Understanding triangles, right triangles, and trigonometric formulas is essential.
Practice regularly, understand geometric principles, and familiarize yourself with various problem scenarios. Online resources and mock tests can be valuable tools.
RELATED POSTS
This was all about the “50+ Height and Distance Questions and Answers”. For more such informative blogs, check out our Study Material Section, or you can learn more about us by visiting our Indian exams page.
 One app for all your study abroad needs
One app for all your study abroad needs













