LCM and HCF for Competitive Exams

Every competitive exam comprises some commonly included sections such as quantitative aptitude and logical reasoning that aim to assess the candidate’s critical thinking and analytical skills. Many students find the quantitative aptitude section complex and confusing because it centrally comprises basic and advanced mathematical concepts. You need to have a good grasp of foundational concepts of Mathematics in order to ace the quantitative aptitude questions. One such foundational concept is LCM and HCF which are mainly a part of mathematical topics covered during the secondary education level. If you need to brush up on your knowledge of these two concepts, this blog aims to provide you with a complete guide on effectively solving questions regarding LCM and HCF for competitive exams.

LCM and HCF are those mathematical concepts that we learn in 5th or 6th standard. So, by the time we start preparing for competitive exams, students often forget what these two are and need to relearn them. These are generally concerned with calculating the common factors and multiples of any two numbers. Let’s take a detailed look at what LCM and HCF mean:

What is LCM? 

LCM stands for Lowest Common Multiple of two or more numbers. For example, if we take two small numbers 3 & 5, their LCM would be 3*5, i.e. 15. This would be the smallest possible positive number that would be divisible by both 3 and 5. This can be understood by, 

Multiples of 3 – 3,6,9,12,15,18,21,24,27,30,…..

Multiples of 5 – 5,10,15,20,25,30,35,40,……

Here, the Lowest Common Multiple, i.e. LCM of 3 and 5 would be 15. 

What is HCF?

HCF stands for Highest Common Factor of a set of numbers. It is also known as the greatest common divisor. For instance, there are three numbers like 10, 12 and 18. We will begin with finding their common factors:

Factors of 10 – 2x5

Factors of 12 – 2x2x3

Factors of 18 – 2x3x3

The highest common factor that these three numbers share is 2 which is their HCF.

If you want to find out the HCF of two or more numbers, you need to define each number as a product of the smallest possible number that is its factor, i.e. break it down to the level of a prime number and write it as its power.

LCM & HCF Problems Explained

Now that we know these concepts separately, it would be easier to solve those questions in which you might be asked to find the HCF as well as LCM of a number. For simplifying these questions of LCM and HCF for competitive exams, there are two methods you can use:

Factorization Method

Factorization method can be extremely useful for easily calculating LCM and HCF. While working on HCF problems, you need to break any of the given numbers in terms of the product of prime factors. Then, find the common factors of those prime numbers. Now, if you multiply those factors, you would get the HCF of the given numbers. For instance, you need to find the HCF of 36 (2×2×3×3×1) and 48 (2×2×2×2×3×1). Start with finding the prime numbers under their common factors, which would be 2, 2 and 3. If you multiply 2, 2 and 3, i.e. 12, it would be the HCF of 36 and 48.

Similarly, for LCM problems, you need to do the same thing by starting with finding the common prime factors then find those numbers that occur the most number of times and calculate how many times they are recurring. To take the same problem as above, the prime factors for 36= 2×2×3×3×1 and 48 = 2×2×2×2×3×1. In this, take a look at how commonly which numbers are occurring. Here, 2×2×3×2×2×3 are amongst the common multiples of both these numbers. Thus, the LCM of 36 & 48 would be 144. Thus, using factorization method, you can simplify the factors and multiples of different numbers which will further assist you in effectively solving the LCM and HCF for competitive exams.

Division Method

The division method for LCM and HCF for competitive exams is a little complex but once you understand it, it can be an effective time-saver. To find HCF of any two numbers, start with dividing the larger number by the smaller one. Then, you need to divide the divisor by the number which is remainder. Keep following the same procedure of dividing the preceding number by its common remainder under the remainder you have is zero. Then, your last divisor would be the HCF of those two numbers. Let’s take 18 & 24. Begin with dividing 24 by 18, the remainder is 6. Then, we will divide 18 by 6 with which you will get zero as the remainder and the divisor for the same is 6 which is also the HCF.

When it comes to simplify the LCM calculation through division method, start with highlighting the least prime number of the given two numbers. For instance, if we take 18 & 24, their least prime number is 2. Divide the two numbers by 2, then find another common prime number, which would be 3, divide the remaining quotients by 3 and then you will get 3 and 4 and so on. Keep dividing the remaining factors until you come to 1. Now, accumulate the divisors together, i.e.  2 × 2 × 3 × 2 = 24. Thus, the division method is another useful way of answering LCM and HCF questions as it only demands you to be aware of the different factors of numbers and further saves time.

How to find LCM and HCF?

Here are the methods we can use to find the HCF and LCM of given numbers:

1. Prime Factorisation Method
2. Division Method

Prime Factorisation for HCF

Let’s explain it by taking an example. Find the HCF of 144,104 and 160

Let’s write the prime factors of the above, 

144 = 2 x 2 x 2 x 2 x 3 x 3
104 = 2 x 2 x 2 x 13
160 = 2 x 2 x 2 x 2 x 2 x 5

The common factors are: 2 x 2 x 2 = 8
Therefore, HCF = 8

Division Method to find the HCF

Steps to find the HCF of any given nos: 

• Large number / Small number
• The divisor of the above step / Remainder
• The divisor of step 2 / remainder. Keep doing this step till R = 0
• The last step’s divisor will be HCF.

Let’s take an example, Find the HCF of 144 and 160

Since 160>144, so the dividend will be 160 & the divisor will be 144. 

Hence, 16 is the highest number which divides 140 and 144. 

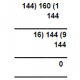
Therefore, HCF = 16

LCM by Prime Factorisation

Let’s find out the LCM of two numbers 60 & 45

Prime factors of each number first, 

60 = 2 x 2 x 3 x 5
45 = 3 x 3 x 5

Multiply those who are occurring the most no of times, 

2 = two times
3 = three times
5 = one time
LCM = 2 x 2 x 3 x 3 = 5

LCM by Division Method

Let’s solve LCM of 60, 45 by division method

Therefore, LCM = 2 x 2 x 3 x 3 x 5 = 180

Solved Samples of LCM & HCF 

Answer: C

Solution: 
Note: LCM of fraction = LCM of numerators / HCF of Denominators
Numerators = 36, 48 and 72.
72 is the largest number among them. 72 is not divisible by 36 or 48
Start with a table of 72.

72 x 2 = 144 = divisible by 72, 36 and 48
∴ LCM of numerators = 144
Denominators = 225, 150 and 65
We can see that they can be divided by 5.
On dividing by 5 we get 45, 30 and 13
We cannot divide further.
So, HCF = GCD = 5

Answer: A

Solution: 

Numerators = 36, 48 and 72.
We can see that they can be divided by 12.
On dividing by 12 we get 3, 4, and 6.
We cannot divide further.
∴ HCF = GCD of numerators = 12
150 is the largest number among them. 75 can divide 150, so neglect 75
Let’s find LCM of 150 and 135
———————————-
5           150           135
———————————-
3           30             27
3           10             9
             10             3
———————————-

∴ LCM of denominators = 5 x 3 x 3 x 3 x 10 = 1350

HCF of fraction =12/350

3. Given : Three numbers 17, 42 and 93

Find the largest number to divide all the three numbers leaving the remainders 4, 3, and 15 respectively at the end?

a. 13
b. 17
c. 78
d. 89

Answer: A

Solution:

Here greatest number that can divide means the HCF
Remainders are different so simply subtract remainders from numbers
17 – 4 = 13; 42 – 3 = 39; 93 – 15 = 78
Now let’s find HCF of 13, 39 and 78
By direct observation, we can see that all numbers are divisible by 13.
∴ HCF = 13 = required greatest number

4. Find the smallest number which leaves the remainders 13, 41 and 29 at the end when divided by 20, 48 and 36 respectively.

a. 187
b. 713
c. 720
d. 727

Answer: B

Solution: 
—————————————–
4           20           36           48
—————————————–
3           5             9             12
             5             3             4
—————————————–
LCM = 4 x 3 x 5 x 3 x 4 = 720
If we observe closely, the difference between the given numbers and remainders is the same
20 – 13 = 7; 48 – 1 = 7; 36 – 29 = 7
The difference is the same = 7
So, simply subtract this difference from LCM.

5. A number when divided by 36, 24 and 16, leaves the remainder 11 in each case. Find the smallest value of this number.

a. 36
b. 133
c. 144
d. 155

Answer: D

Solution
We must first find LCM of 36, 24 and 16
————————————–
4           16           24           36
————————————–
3           4             6              9
2           4             2              3
             2             1              3
————————————–
∴ LCM = 4 x 3 x 2 x 2 x 1 x 3 = 144
Since remainder is same just add it to this LCM
Number = 144 + 11 = 155

LCM and HCF for Competitive Exams: Tips & Tricks

LCM and HCF are some of the elementary concepts that you need to brush up while preparing for maths for competitive exams. Below we have listed down some of the helpful tips and tricks that you can utilise while gearing up for problems related to LCM and HCF for competitive exams.

• Practise, Practise and Practise: Maths has only one success mantra which is that you need to consistently practise different kind of questions for every concept in order to strengthen your grasp on it. So, take up practise papers, identify the kind of questions asked under LCM and HCF and then solve a varied range of problems that will help you master these two concepts. 
• Memorise the Tables: Learn the multiplication tables till at least 30 which would come in handy for finding factors for LCM and HCF and it would also save your time spent in calculations.
• Prepare a Flowchart: A flowchart is a really important thing from the perspective of cracking questions of LCM and HCF for competitive exams. Prepare flowcharts of different multiplication tables, prime numbers, factors as well as different methods which will help you navigate through the crucial concepts for a quick revision. 
• Time Management: It would be highly improbable if someone does not mention time management as a tip while suggesting you a way around the quantitative ability section. So, you must attempt mock tests and other practice papers to prepare for the section of LCM and HCF for competitive exams. Also, time yourself while giving every mock tests and keep a tab on how many minutes you are spending on each question.

Also Read

• Statistics Class 9 Maths Study Notes
• Surface Area And Volume Class 10 Maths
• Partnership Questions
• Analytical Reasoning For Competitive Exams

Thus, we hope that this blog helped you understand the key essentials of effectively solving LCM and HCF for competitive exams. If you are planning to appear for any competitive exam such as GMAT, GRE, etc, you can always get in touch with our Leverage Edu experts and we’ll help you prepare for every section of your chosen exam, along with providing you with the right study materials and important tips. Leverage edu also provides information about study abroad for Indian students who want to make their career abroad.