Class 9 Lines And Angles NCERT Notes

Class 9 Chapter 6 Lines and Angles is an essential chapter that aims to create a sound foundation for the upcoming chapters of geometry. It introduces the students to the elementary concepts of lines and angles as understanding them will assist you in solving complex questions of geometry. With its application in a wide variety of topics and concepts, it is essential to go through this chapter of the class 9 maths syllabus. Hence, through this blog, we aim to highlight the key features of class 9 lines and angles. 

Basic Definitions and Terms

The ideal way to begin with the chapter is to understand and learn the important definitions and terms of the chapter. Mentioned below are some vital definitions of varied types of lines and angles.

Line Segment 

If a line has two ends, then it is called a line segment. 

Ray

That part of the line with one endpoint is called a ray.    

Non-Collinear Points

It is an essential concept of class 9 lines and angles, which says that collinear points are present in a line having three or more points. Else, they are called non-collinear points. In simpler terms, non-collinear points do not allow a single line to be formed through them. 

Must Read: Vedic Maths Rules to Reduce Calculations

Now let us have a look at the types of angles that we will be studying in this chapter.

Types of Angles 

When two rays originate from the same endpoint, it is called an Angle. Arms are the two rays that make the base for an angle. The endpoints where the two rays meet are known as the Vertex. 

There are various types of angles, explained below are the important ones according to the class 9 lines and angles chapter.

Also Read: CBSE Class 10 Maths Syllabus

Acute Angle

All the angles that measure between the range of 0 to 90 degrees are called acute angles. 

Right Angle

As per the class 9 lines and angles chapter, an angle which measures exactly 90 degrees is called a Right Angle.

Obtuse Angle

This is an angle greater than 90 degrees but smaller than 180 degrees.

The picture given below depicts a comparison between the 3 main types of angles. 

Here are some class 9 Coordinate Geometry Formulas for you!

Reflex Angle

A reflex angle is greater than 180 degrees but less than 360 degrees.

Complementary Angles

Two angles having a sum of 90 degrees are called complementary angles.

Supplementary Angles

It happens to be an important concept of class 9 lines and angles. Supplementary angles are those angles which have some 180 degrees.

Adjacent Angles

Two or more angles that have a common vertex are called adjacent angles.

Linear Pair Angles

It is a fundamental concept of this chapter and it says that if two non-common arms say, a and b can form a line,  they will be called line pair angles. 

Word Problems on Arithmetic Operations

Vertically Opposite Angles

When two lines, say, AB and CD intersect one another, they are called vertically opposite angles. 

If there are two lines parallel to one another and have the same length or perpendicular on the surface of the line, it is called the distance between two parallel lines. The vertically opposite angle is an elementary concept of lines and angles.

Transversal Lines

A transversal line is one that intersects two or more lines at distinct points.

Axioms of Lines and Angles  

For all of us to solve the questions of the lines and angles class 9, there are some axioms that have been laid down. All the steps that are involved in the solution of a question must be in accordance with these axioms. 

Also Read: Perfect Squares

Line Pair Axiom

The non-common arms of the angle will always form a line whenever the sum of two adjacent angles is more than 180 degrees. 

Corresponding Angles Axiom

When two lines are intersected by a transversal forming two corresponding angles in pairs, they will be parallel to one another. 

Consecutive Interiors     

They are the angles that lie on the same transversal side. They are also called allied or co-interior angles. 

Theorems of Class 9 Lines and Angles 

Just as the axioms of the lines and angles are important while solving a question, similarly, one must keep in mind these theorems.

Theorem 1

When two lines that have a pair of alternate interior angles that are equal are intersected by a transversal, then the two lines are always parallel.

Theorem 2

A pair of interior angles on the same transversal’s side on two parallel lines will be supplementary whenever a transversal intersects.

Theorem 3

If two interior angles are formed on the same side of a transversal and are supplementary to each other and have a transversal interesting the two parallel lines, then those two lines are parallel.     

Theorem 4

The Sum of all the angles of the triangle is 180 degrees.

Theorem 5 

The sum of two interior opposite angles of a triangle is always equal to the exterior angle of the triangle.

Must Read: Math tricks to ace your exams! 

Class 9 Lines and Angles Solved Examples NCERT

Listed below are some of the solved examples from NCERT that will help you in getting a better hold on this topic-

Example 1: In the figure, lines XY and MN intersect at 0. If ∠POY = 90°, and a: b = 2 : 3. find c.

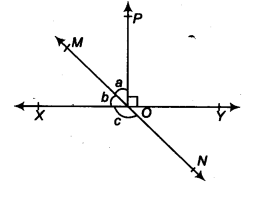
Solution:
Since XOY is a straight line.
∴ b+a+∠POY= 180°
But ∠POY = 90° [Given]

∴ b + a = 180° – 90° = 90° …(i)
Also a : b = 2 : 3 ⇒ b = 3a/2 …(ii)
Now from (i) and (ii), we get

3a/2 + A = 90°
⇒ 5a/2 = 90°
⇒ a = (90/5)x 2= 36 = 36°

From (ii), we get
b = (3/2) x 36° = 54°
Since XY and MN interstect at O,
∴ c = [a + ∠POY] [Vertically opposite angles]
or c = 36° + 90° = 126°

Thus, the required measure of c = 126°.

Example 2: In the figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that: ∠ROS= 1/2 (∠QOS- ∠POS)

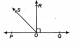
Solution 2:

POQ is a straight line. [Given]
∴ ∠POS + ∠ROS + ∠ROQ = 180°

But OR ⊥ PQ

∴ ∠ROQ = 90°
⇒ ∠POS + ∠ROS + 90° = 180°
⇒ ∠POS + ∠ROS = 90°
⇒ ∠ROS = 90° – ∠POS … (1)
Now, we have ∠ROS + ∠ROQ = ∠QOS

⇒ ∠ROS + 90° = ∠QOS
⇒ ∠ROS = ∠QOS – 90° ……(2)

Adding (1) and (2), we have

2 ∠ROS = (∠QOS – ∠POS)

∴ ∠ROS = 1/2(∠QOS−∠POS

Example 3: In the figure, find the values of x and y and then show that AB || CD.

Solution: y = 130° …(1)
[Vertically opposite angles]

Again, PQ is a straight line and EA stands on it.
∠AEP + ∠AEQ = 180° [Linear pair]
or 50° + x = 180°

⇒ x = 180° – 50° = 130° …(2)
From (1) and (2), x = y
As they are pair of alternate interior angles.

∴ AB || CD

Class 9 Lines and Angles Free PDF

We have attached a free notes PDF for this chapter, to help you understand better.

Points to Remember

To sum up, in this chapter on lines and angles for class 9 you will learn that-

• The sum of two angles adjacent to one another so formed is 180 degrees and vice versa if a ray stands on the line. This property is popularly known as the Linear Pair axiom
• When two lines intersect one another then the vertically opposite angles so formed are equal
• In the incident that a transversal intersects two parallel lines then each pair of corresponding angles are identical. Moreover, the alternate interior angles in pairs are equal.    
• If two lines intersect, each other then any one pair of corresponding angles is equal, or anyone pair of alternate interior angles is identical, and anyone pair of interior angles on the same side of the transversal is supplementary then the lines are parallel 
• Lines that are parallel to a given line are also parallel to each other
• The Sum of the three angles of a triangle is 180 degree
• When a triangle’s side is produced, the resulting exterior angle formed is the same as the sum of two interior opposite angles.    

Also read: Motion science study notes

Class 9 Lines and Angles Extra Questions

Here are some questions for practising lines and angles of class 9:

1. Prove that the sum of three angles of a triangle is 180 degrees.
2. What is a ray? 
3. Explain what are corresponding angles, alternate angles, and vertically opposite angles.
4. What is a reflex angle?
5. What is a vertex?
6. What are consecutive interiors?
7. What is a ray? 
8. Prove that if a line has a ray, then the sum of the two angles formed is 180 degrees. 
9. PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB CD.

Class 9 Lines and Angles Worksheet

Now that we have discussed the chapter in detail, here is a worksheet for your practice.

FAQs

We hope that through this explanation of lines and angles for the very important class 9, you are through with this concept. If you want to get familiar with the most advantageous career path as per your interests, get in touch with our Leverage Edu experts.