Boats and Streams Formula

Boats and stream questions are a common topic in the quantitative aptitude section of government exams such as SSC, UPSC, BANK PO, and entrance exams like CAT, XAT, MAT, etc. Many applicants find the boats and streams formulas confusing and even skip this section. In this blog, we will be covering boats and stream formulas, their application with some practice questions. 

Also Read: A Guide On How to Prepare for Bank Exams

Important Terms for Boats and Streams Formula

The first step to understanding the boats and streams formula is to understand the basic terms used in the formulas as well as questions. Here are the important terms every applicant should know:

1. Stream- The water that is moving in the river is called a stream.
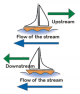
2. Upstream- When the boat is flowing in the opposite direction of the stream, it is called Upstream.
3. Downstream- When the boat is flowing in the same direction as the stream, it is called Downstream
4. Still Water- When the water is stationary i.e. not flowing then the speed of water is zero. 

Also Read: Permutation And Combination For Competitive Exams

Boats and Streams Formula

Without knowing the accurate boats and streams formula it is impossible for any applicant to solve the question. Every applicant should memorize these and should be on fingertips. Here are some of the important boats and stream formulas:

Upstream	(u−v) km/hr
Downstream	(u+v)Km/hr
Speed of Boat in Still Water	½ (Downstream Speed + Upstream Speed)
Speed of Stream	½ (Downstream Speed – Upstream Speed)
Average Speed of Boat	{(Upstream Speed × Downstream Speed) / Boat’s Speed in Still Water}
Speed of boat or swimmer in still water	1/2 (Downstream Speed + Upstream Speed)

Other Important Boats and stream formulas

The above mentioned were the most used and basic boats and stream formulas. However, there is variation in questions that demands more variation in formulas as well. Here are some other important boats and stream formula:

• Calculating distance between two points, If it takes “t” hours for a boat to reach a point in still water and comes back to the same point
  
   Distance = {(u2-v2) × t} / 2u

• Calculating the distance between two points, If it takes “t” hours more to go to a point upstream than downstream for the same distance
  
  Distance = {(u2-v2) × t} / 2v

• Calculate the speed of swimmer or man in still water, If a boat travels a distance downstream in “t1” hours and returns the same distance upstream in “t2” hours
  
  [v × {(t2+t1) / (t2-t1)}] km/hr
  u= speed of the boat in still water 
  v= speed of the stream

Also Read: Banking Courses after Graduation

Types of Boats and Stream Questions

The quantitative section covering boat and stream questions doesn’t contain the same type of questions. There are 4 types of questions and based on the type, boats and stream formula is applied accordingly:

• Time-based questions
• Speed based questions
• Average speed based questions
• DIstance based questions

1. Time-based questions: As the name suggests, you have to calculate time in this type of question. You will have to calculate the time taken by a boat to travel upstream or downstream.

Example – The speed of a boat is that of the stream as 36:5. The boat goes along with the stream in 5 hours and 10 minutes. How much time will it take to come back?

Solution:  6 5/6

2. Speed-based questions: In this type, you have to calculate the speed of the stream or boat. In this type of question, you might also find variations such as the speed of the boat in still water.

Example – The speed of the boat when traveling downstream is 32 km/hr. whereas when traveling upstream it is 28 km/hr. What are the speed of the boat in still water and the speed of the stream?

Solution :  Speed of the boat in still water = 30 km/hr.

Speed of the stream = 2 km/hr.

3. Average speed-based questions: This is the simplest type, the speed of downstream and upstream will be mentioned and you have to find out the average speed. Sometimes, the speed of either one stream is mentioned with the average speed and you will have to calculate the other speed of the other stream.

Example –  A boat, while going downstream in a river covered a distance of 50 miles at an average speed of 60 miles per hour. While returning because of water resistance, it took 1 hour 15 minutes to cover the same distance. What was the average speed during the whole journey?

Solution :  48 miles/ hr.

4. Distance-based questions – In this type, you have to calculate the distance traveled by boat upstream or downstream. Usually in this type of question time, speed and stream are mentioned.

Example –  A person challenged himself to cross a small river and back. His speed of the boat in still water is 3 km/hr. He calculated the speed of the river that day as 1 km/hr. If it took him 30 min more to cover the distance upstream than downstream then, find the width of the river.

Solution:  2 Km

Also Read: RBI Grade B Exam

Tips and Tricks for Boats and Stream Questions

Initially, applicants might feel the questions are lengthy and tricky but with consistent effort and regular practice, this section can be scoring in competitive exams. Here are some tips and tricks for boats and stream questions:

1. Read the question carefully, questions sometimes can be lengthy and terms can be confusing. Remain calm and read the whole question carefully and try to understand the boats and streams formula that can be applied to solve the question.
2. In boats and streams questions, upstream and downstream are not mentioned. Don’t let it confuse you. Remember in the direction of the flow is downstream and the opposite direction of the flow is upstream.
3. You will only be able to solve these questions if you have memorized the boats and streams formula. Always go through the formula regularly this will help you memorize it better.
4. At last, practice makes the students perfect. Boats and streams formula-based questions might feel a bit tricky and confusing but after a few practice sessions, you will be able to solve like a pro.

Also Read: Tips to Crack Competitive Exams

Practice Questions

Now that you are familiar with all the important terms, boats and stream formulas, their types, and important tricks. Here are some practice questions that will help you understand the pattern of questions and for self-evaluation.

• In one hour, a boat goes 11 km along the stream and 5 km against the stream. The speed of the boat in still water (in km/hr) is: 

1.  3                     
2. 5                    
3. 8                
4.  9                
5. 11

Answer: 8

• A certain boat downstream covers a distance of 16 km in 2 hours downstream while covering the same distance upstream, it takes 4 hours. What is the speed of the boat in still water?  

1. 4 km/hr                       
2. 6 km/hr                          
3. 8 km/hr                       
4. Data Inadequate         
5. None of these

Answer: 6 km/hr

• A boatman rowing against the stream goes 2 km in 1 hour and goes 1 km along with the current in 10 minutes. How long does it take him to go 5 km in stationary water?  

1. 40 minutes                 
2. 1 hour                     
3. 1 hr 15 minutes                  
4. 1 hr 30 minutes                      
5. None of These

Answer: 1 hour 15 minutes

• A boat takes 90 minutes less to travel 36 miles downstream than to travel the same distance upstream. If the speed of the boat in still water is 10 mph, the speed of the stream is:   

1.  2 mph
2. 2.5 mph
3. 3 mph 
4. 4 mph
5. None of These

Answer:  2 mph  

•  If Rajiv rows at his usual rate, he can travel 12 miles downstream in a certain river in 6 hours less than it takes him to travel the same distance upstream. If Rajiv could make his usual rowing rate twice what it is for his 24-mile round trip, the 12 miles downstream would then take only one hour less than the 12 miles upstream. What is the speed of the current in miles per hour?

1. 1(1/3)                          
2. 1(2/3)                            
3. 2(1/3)                            ‘
4. 2(2/3)

Answer: 2(2/3)

FAQs

This was all about the Boats and streams formula. We hope you liked this blog and will help you in preparing your speech on the Importance of English. For the latest updates around study blogs, you can follow us on Instagram, Twitter, Facebook and also subscribe to our newsletter. Leverage Edu wishes you all the best for all your future endeavors.