One app for all your study abroad needs
The Fibonacci Series is a popular sequence that is named after Leonardo Pisano Bogollo, an Italian Mathematician. However, its application is not limited to the world of mathematics only. Instead, it extends beyond the mathematical sphere to other aspects of our lives such as finance, music, engineering, cryptography, and the animal world as well. In this blog, we will explore the amusing details of the Fibonacci series or Fibonacci sequence, its formula, and how it has uses in diverse fields. Let’s begin with the basics first.
Table of Contents
Also Read: What is Raman Effect in Simple Words?
What is Called the Fibonacci Series?
In layman’s language, the Fibonacci Series is an arrangement of numbers which is also referred to as the Fibonacci numbers. To understand this specific pattern of numbers, imagine a special arrangement of numbers where each number is created by simply adding the two numbers before it. This sequence begins with 0 and 1 and continues like 0, 1, 1, 2, 3, 5, 8….Here you can easily spot that you can calculate the next number by adding the two previous numbers. For example, to find the 6th number in a Fibonacci sequence, you just have to add the 4th and 5th numbers.
To make things simpler, let us assume that the first term F0 is 0 and the second term F1 is 1, here is how to find the third term:
F2= F0 + F1
F2= 1
Similarly, you can find the other terms of the series by simply applying the above-mentioned concept.
Also Read: 📊What is Anomaly Detection in AI and Why is it Important?
Fibonacci Series Formula
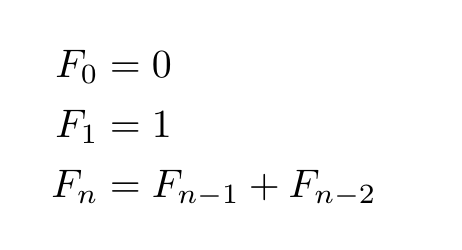
As you can see, the Fibonacci series formula can be used to calculate and find the missing terms or numbers in the series. The most common way to do that is by completing the Fibonacci series using recursion such that the Fn term can be found by simply adding the preceding two terms.
Fn = Fn-1 + Fn-2,
where n > 1
Also Read: Famous Mathematician of All Times
What is the Fibonacci Spiral?
The Fibonacci series in nature is an amusing concept to understand. The Fibonacci spiral is a mathematical pattern that intricately bears a resemblance to a swirling curve. To create this logarithmic spiral, the corners of squares that have side lengths corresponding to the numbers in a specific Fibonacci sequence are connected.
logarithmic spiral that is simply formed by joining the corners of squares that have side lengths the same as the numbers in a specific Fibonacci sequence. This spiral makes frequent appearances in nature, especially in the arrangement of seeds in sunflowers, leaves on a stem, the shell of a nautilus, the galaxies, and so on.
Applications
Below we have jotted down the numerous applications of the Fibonacci series. Let’s take a look at them one by one:
- The Fibonacci series can be used in engineering such as data structures, sorting algorithms, trading algorithms, etc.
- It is also used in music to create melodies and musical patterns.
- It can be used to create mathematically precise yet beautiful and captivating paintings and sculptures.
- Biomimicry is another application of the Fibonacci series where engineers learn to create efficient products using patterns and arrangements found in nature.
Also Read: What Does URL Stand For?
Fibonacci Series Golden Ratio
Did you know that the Fibonacci Series is closely related to the value of the Golden Ratio? How? Well, to begin with, we already know that the value of the Golden Ratio is approximately 1.618034. Moreover, it is represented by using the ϕ symbol. So, if we take the ratio of two successive Fibonacci numbers (of bigger value) in a series, the ratio will be close to the Golden Ratio.
For instance, the ratio of 34 and 21 is:
34/21 = 1.619
In the same way, you can find the Fibonacci numbers using the Golden Ratio. For that, here is the formula:
Xn = [φn – (1-φ)n]/√5
| Symbol | Description |
| φ | It is the Golden Ratio which is equal to 1.618 approximately. |
| n | The nth term of a Fibonacci sequence. |
Related Blogs
FAQs
The first 20 terms in the Fibonacci series are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181.
1 1 2 3 5 8 is the Fibonacci series in which a number can be easily found by simply adding the two numbers before it.
To solve a Fibonacci sequence, you can use the Fn = Fn-1 + Fn-2 formula where n is greater than 1.
This blog was all about the Fibonacci series. For more information about such informative articles, make sure to check the trending events page of Leverage Edu.