Pythagoras Theorem

Various concepts of mathematics such as Profit and Loss, Simple Interest, Compound Interest, etc are not only an integral part of our school lives but also essential for various entrance and competitive exams. Another popular topic belonging to the same group is the Pythagoras Theorem which has a vital significance in our day to day lives as well as constitutes to be an imperative mention in the syllabus of scholastic and competitive exams. Are you facing trouble in understanding this topic? Don’t Worry! This blog aims to elucidate the concept of it as well as some practice questions.  

[powerkit_toc title=”This Blog Includes:”]

What is Pythagoras Theorem?

In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides. The is the Pythagoras theorem which only works for the right-angled triangles. The sides of a right-angled triangle are called – Perpendicular, Base and Hypotenuse. Here, the side that is opposite to the 90-degree angle is the hypotenuse which is the longest side. 

Did you know: The Pythagoras Theorem is named after a greek Mathematician called Pythagoras!

Pythagoras Theorem Formula 

Named after the Greek mathematician Pythagoras, the Pythagoras formula gives out the measurement of the side by calculating the other two sides of a triangle. According to the above-mentioned Pythagoras theorem, the Pythagoras formula is:

Hypotenuse² = Perpendicular² + Base²

It can be simply written as, c² = a² + b²

In the formula, 

a is the perpendicular side 

b is the base

c is the hypotenuse side 

Let us observe the above-mentioned image which comprises of 3 squares on the 3 sides of a triangle. The a, b, c squares are different in their size as per the side they are on. According to the Pythagoras formula, 

Area of Square a + Area of Square b = Area of Square c

Hence, for any right-angled triangle, the c square i.e., on the longest side of the triangle has the exact same area as the other two a square and b square. 

Let us go through an example to understand the working of Pythagoras formula-

Proof of Pythagorean Theorem

At a right angle, the square of the hypotenuse is equal to the sum of the squares of the other two sides:

It is written as, a² + b² = c² 
LET QR = a, RP = b, PQ = c

Draw a square of WXYZ of side (b+c). Take points, E, F, G, H on sides WX, XY, YZ, and ZW, such that WE = XF = YG = ZH = b

Then we will get 4 right-angled triangles, the hypotenuse of each of them is ‘a’

The remaining sides of each of them are C

The remaining part of the figure is square EFGH, is a²

Now, we are sure that, 

square WXYZ = square EFGH + + 4 ∆ GYF

or, (b + c)² = a² + 4 ∙ ¹/₂ b ∙ c

or, b² + c² + 2bc = a² + 2bc

or, b² + c² = a²

Pythagorean Triples

The three positive numbers that entirely satisfy the Pythagorean theorem are known as Pythagorean triples. The theorem claims that the square of the hypotenuse in every right triangle is equal to the sum of the squares of the other two legs. The Pythagorean triples are made up of the three sides of a right triangle. Let’s learn how to swiftly construct a few Pythagorean triples. 

The most popular example of Pythagorean triples is (3, 4, 5). We can verify that 3, 4 and 5 satisfy the equation a² + b² = c². Let’s see how!

3² + 4² = 5² ⇒ 9 + 16 = 25

Rule: Pythagorean triples are a set of positive integers which satisfies a² + b² = c²           

Examples of Pythagorean Triples

The Pythagorean triples set is infinite. The first Pythagorean triples have been identified as (3, 4, and 5). By scaling them up in the following way, we can generate a few additional triples. Taking values for n allows us to make as many triples as feasible.

n	(3n, 4n, 5n)
2	(6, 8, 10)
3	(9, 12, 15)
4	(12, 16, 20)
5	(15, 20, 25)

List of Pythagorean Triples

Given below is a list of some popular Pythagorean Triples that satisfies the Pythagoras Theorem. 

(3, 4, 5)	(5,12,13)	(7, 24, 25)
(8, 15, 17)	(9, 40, 41)	(11, 60, 61)
(12,35, 37)	(13, 84, 85)	(15, 112, 113)
(16, 63, 65)	(17,144, 145)	(19, 180, 181)
(20, 21, 29)	(20, 99 ,101)	(21, 220,221)

Applications of Pythagoras Theorem

Apart from solving mathematical questions, we can use formulas for various things. Pythagoras theorem is not just limited to our maths textbooks. It is often used in various activities of daily lives. Major useful applications of Pythagoras Theorem are:

• Used in Engineering and Construction Fields: When length or breadth are known, it is fairly easy to determine the diameter of a certain sector. Most builders use the Pythagorean theorem to find the value. In engineering applications, it is primarily employed in two dimensions.
• Used as Face Recognition in Security Cameras: Face recognition is becoming increasingly common these days, and it helps to cut the amount of time it takes to investigate crimes in the security sector. It goes through the Pythagorean theorem concept, which means that the distance between the security camera and the location where the person is noticed is well projected through the lens.
• Woodworking and Interior Designing: As the basic notion suggests, if square cardboards can be easily turned into triangles by cutting diagonally, the Pythagoras concept can be easily used. The majority of woodworks are created using an approach that makes it easier for designers to move forward.
• Navigation: It’s a fascinating truth, but people going by sea utilise this technique to determine the quickest distance and route to their destinations.
• Surveying: Typically, surveyors use this technique to locate the steep hilly zone; once they have the horizontal region, they may apply the Pythagoras principle to compute the rest. The surveyor can gaze through a telescope at the fixed and changing distances, making the journey easier.

Hence, all those who aspire to enter these fields after class 12th must have a strong grip over the topic. 

Pythagoras Theorem PPT

Pythagoras theorem ppt from Gaurav1721

Before we move on to some solved examples on the Pythagoras theorem,
let us have a look at the Ratio and Proportion Questions!

Solved Examples 

Now that you are familiar with the formula it’s working, let us have a look at some unique questions. The below-mentioned questions are highly important from the competitive exam point of view. Here are some solved examples in detail- 

Example 1: Find the length of the sides, if the hypotenuse of an isosceles right-angled triangle is 128 cm2. 

Solution:

Before we begin with solving this problem, we would like to bring your notice to the statement ‘isosceles right-angled triangle’. An isosceles triangle has 2 equal sides, thus, an isosceles right angle triangle will have an equal base and perpendicular. The length of the hypotenuse will be different.

Now, let the 2 equal sides of the triangle be x cm.

It is given that h^2 = 128 cm 
So from the image,

PR^2 = PQ^2+ QR^2
h^2 = x^2+x^2
128 = 2x^2
128/2 = x^2
64 = x^2
Sq Root (64) = x
8= x

Therefore both PQ and QR are 8 cm long!

Here are some Seating Arrangement Questions for Competitive Exams
to help hit a higher score in these exams!

Example 2: Ram drove his car 100m from point A in the Northeast direction to the B. He further moves to the west of Y and reaches point Z. Point Z is located exactly at the north of the A at a distance of 60 m. Find the distance between A and Y. 

Solution: 
Let the length of AY= x m 
Hence, YZ= (100-x) m 

In the triangle XYZ, angle Z= 90 degree

Therefore, according to the Pythagoras theorem:
AY^2=YZ^2 + ZA^2
 x^2= (100- x^2) + 60^2
x^2= 1000 – 200x + x^2 3600

In the aforementioned step, we have eliminated the term x2 from LHS and RHS
200x = 10000 + 3600 
x= 13600/ 200
x= 68 
Thus, the distance between A and Y= 68m 

Example 3: In the below-mentioned image, the size of the perpendicular is 5 cm and the size of the base is 12 cm. Determine the size of the hypotenuse. 

Solution:

As we have to find the length of the longest side, we will begin by using the formula- 
c^2=a^2 + b^2
c^2= 5^2 + 12^2 
c^2= 25+ 144 
c^2= 169
c= Sq Root (169)
= 13
Hence, the length of the hypotenuse is 13 cm 

Have a look at these Algebra Questions!

Pythagoras Theorem Practise Questions 

Since we are through with the concept and formula of the Pythagoras theorem, now its the time to practice some questions. 

Q1: A rectangular park has a length of 150m. A diagonal footpath has a length of 170m. Calculate the perimeter using the Pythagoras formula

Q2: There are 2 buildings which have a height of 39 and 24m. If the distance between those 2 buildings is 10m, calculate the distance between the top of the two buildings

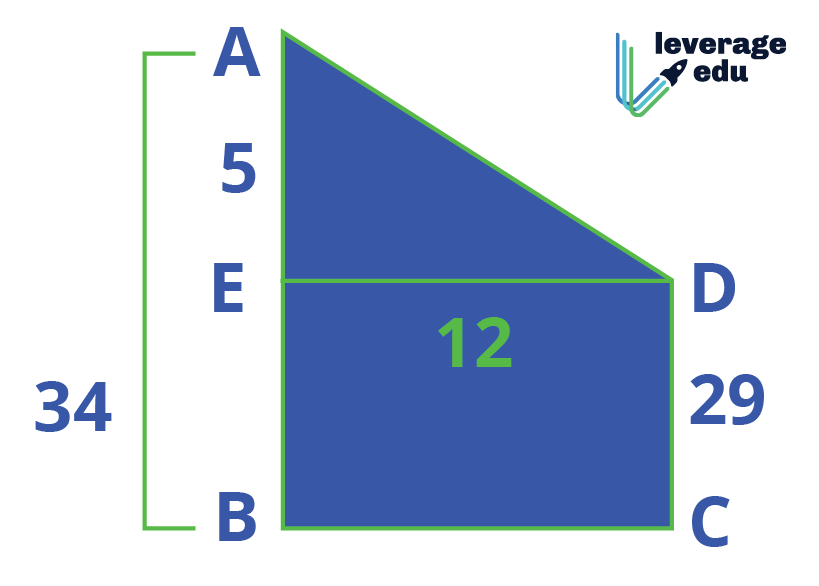
Q3: The two sides of a right-angled triangle are 17m and 15m, determine the third side of the triangle.

Q4: There is a square with a side of 8m. If two corners of it are joined, what will be the length of the diagonal?

Q5: A ladder of height 13m touches the top of a vertical building with a height of 12m. What will be the distance between the ladder and the bottom of the wall

Q6. The side of the triangle is of length 7.5 m, 4 m, 8.5 m. Is this triangle a right triangle? If so, which side is the hypotenuse?

Q7. In ∆ABC right angled at A. if AB = 10 m and BC = 26 m, then find the length of AC.

Q8. In ∆XYZ right-angled at Y. find the length of the hypotenuse if the length of the other two sides is 1.6 cm and 6.3 cm.

Q9. If the square of the hypotenuse of an isosceles right triangle is 98cm, find the length of each side.

Q10. A triangle has a base of 5 cm, a height of 12 cm and a hypotenuse of 13 cm. Is the triangle right-angled?

Pythagoras Theorem Practice Worksheet

FAQs

Thus, we hope that this blog about the Pythagoras theorem has helped you get an idea about this concept. For expert assistance in integral decisions like stream selection after class 10th, reach out to our Leverage Edu experts.