Trigonometry Formulas, Examples and Solutions! 

Trigonometry is the study of relationships between angles and sides of triangles and is a fundamental branch of mathematics. However, Trigonometry Formulas come into use whilst solving trigonometry problems. Furthermore, these Trigonometry Formulas help with the solutions. Read on to learn more about these important Trigonometry Formulas along with their Examples and Solutions. 

Also Read: Introduction to Trigonometry

Basic Trigonometric Ratio Formulas 

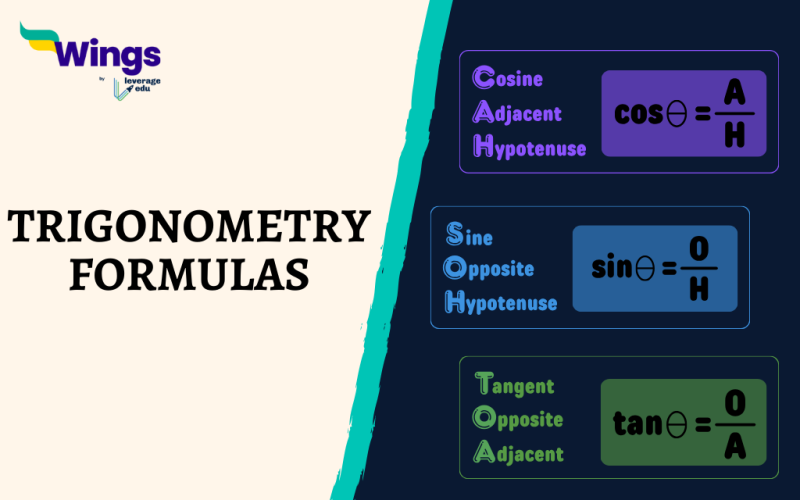
The Basic Trigonometric Ratios are sine (sin), cosine (cos), and tangent (tan). Moreover, these Ratios are defined as follows:

• Sine (sin): The ratio of the opposite side to the hypotenuse of a right-angled triangle.
  • For Example: In a right-angled triangle with an angle of 30°, if the hypotenuse is 10 units, the opposite side is 5 units. 
  • Therefore, sin(30°) = 0.5.

• Cosine (cos): The ratio of the adjacent side to the hypotenuse of a right-angled triangle.
  • For Example: In the same triangle, the adjacent side is 8.66 units. 
  • Therefore, cos(30°) = 0.866.

• Tangent (tan): The ratio of the opposite side to the adjacent side of a right-angled triangle.
  • For Example: In the same triangle, the tangent of 30° is 0.577, as the opposite side is 5 units and the adjacent side is 8.66 units.

Also Read: 21 Trignometry Formulas for Competitive Exams 

Reciprocal Identities 

Additionally, the Reciprocal Identities are:

1. Cosecant (csc): The reciprocal of sine, csc(x) = 1/sin(x).

2. Secant (sec): The reciprocal of cosine, sec(x) = 1/cos(x).

3. Cotangent (cot): The reciprocal of tangent, cot(x) = 1/tan(x).

For Example: 

If sin(x) = 0.5, 

then csc(x) = 1/0.5 = 2.

Also Read: Algebraic Identities: Examples and Chart

Trigonometric Ratio Table

Here is the Trigonometric Ratio Table that provides the values of sine, cosine, and tangent for common angles:

Trigonometric Ratio Table
Angle	Sine	Cosine	Tangent
0°	0	1	0
30°	0.5	0.866	0.577
45°	0.707	0.707	1
60°	0.866	0.5	1.732
90°	1	0	undefined

For Example: If the angle is 45°, the sine is 0.707, the cosine is 0.707, and the tangent is 1.

Also Read: Trigonometry Formulas for Quantitative Section

Periodic Identities 

Moreover, the Periodic Identities describe the repeating patterns of Trigonometric functions:

1. sin(x + 2π) = sin(x)

2. cos(x + 2π) = cos(x)

3. tan(x + π) = -tan(x)

For Example: 

If sin(x) = 0.5, 

then sin(x + 2π) = 0.5.

Also Read: Order of Operations and PEMDAS Rule

Co-Function Identities 

The Co-Function Identities relate the Trigonometric functions of Complementary angles (angles that add up to 90°):

1. sin(x) = cos(90° – x)

2. cos(x) = sin(90° – x)

3. tan(x) = cot(90° – x)

For Example: 

If sin(30°) = 0.5, 

then cos(60°) = 0.5.

Also Read: Conic Sections

Sum and Difference Identities 

The Sum and Difference Identities describe the relationships between Trigonometric functions of the sum or difference of two angles:

1. sin(A + B) = sin(A)cos(B) + cos(A)sin(B)

2. sin(A – B) = sin(A)cos(B) – cos(A)sin(B)

3. cos(A + B) = cos(A)cos(B) – sin(A)sin(B)

4. cos(A – B) = cos(A)cos(B) + sin(A)sin(B)

For Example: 

If sin(30°) = 0.5 and cos(45°) = 0.707, 

then sin(30° + 45°) = 0.5 ✕ 0.707 + 0.866 ✕ 0.707 = 0.866.

Also Read: What is the Difference Between Degrees and Radians?

Half, Double and Triple Identities 

These Identities relate the Trigonometric functions of an angle to the functions of Half, Double, or Triple that angle:

1. sin(2x) = 2sin(x)cos(x)

2. cos(2x) = cos²(x) – sin²(x)

3. tan(2x) = 2tan(x) / (1 – tan²(x))

For Example: 

If sin(30°) = 0.5, 

then sin(60°) = 2 ✕ 0.5 ✕ 0.866 = 0.866.

Also Read: Branches of Mathematics: Arithmetic, Algebra, Geometry, Calculus, Trigonometry, Topology, Probability and Statistics

Sum to Product Identities 

The Sum to Product Identities allows the conversion of sums and differences of Trigonometric functions into products:

1. sin(A) + sin(B) = 2sin((A+B)/2)cos((A-B)/2)

2. sin(A) – sin(B) = 2cos((A+B)/2)sin((A-B)/2)

3. cos(A) + cos(B) = 2cos((A+B)/2)cos((A-B)/2)

4. cos(A) – cos(B) = -2sin((A+B)/2)sin((A-B)/2)

For Example: 

If sin(30°) = 0.5 and sin(45°) = 0.707, 

then sin(30°) + sin(45°) = 2 ✕ sin(75°/2) ✕ cos(15°/2) = 0.866 ✕ 0.966 = 0.837.

Also Read: Profit and Loss Formula Questions

Inverse Trigonometry Formulas 

The inverse trigonometric functions, denoted as sin^-1, cos^-1, and tan^-1, allow us to find the angle given the value of the trigonometric function:

1. sin^-1(x) = the angle whose sine is x
2. cos^-1(x) = the angle whose cosine is x
3. tan^-1(x) = the angle whose tangent is x

For Example: 

If sin(x) = 0.5, 

then x = sin^-1(0.5) = 30°.

Also Read: 20 Most Famous Indian Mathematicians

Sine Law  

The Sine Law states that the ratio of the length of a side to the sine of the opposite angle is constant for all triangles:

sin(A)/a = sin(B)/b = sin(C)/c

For Example: 

In a triangle with sides a = 5, b = 6, and c = 7, and angles A, B, and C, we can use the sine law to find the unknown angle A:

sin(A)/5 = sin(B)/6

sin(A) = (5/6)sin(B)

Also Read: Algebra Questions

Cosine Law

The Cosine Law relates the lengths of the sides of a triangle to the cosine of one of the angles:

c^2 = a^2 + b^2 – 2ab cos(C)

For Example: 

In a triangle with sides a = 5, b = 6, and c = 7, we can use the cosine law to find the angle C:

7^2 = 5^2 + 6^2 – 2(5)(6)cos(C)

cos(C) = (5^2 + 6^2 – 7^2) / (2 * 5 * 6) = 0.5

Related Blogs 

7 Types of Fractions with Examples	What are Co Prime Numbers?
How to Find Percentage of Marks?	Multiplication Tables of 1 to 20
Ordinal Numbers from 1 to 100!	Table of 17: Multiples up to 20 & a Trick!
Table of 12: Multiples up to 20!	What is the HCF of Two Consecutive Odd Numbers?

I hope this helps! Did you like learning about Trigonometry Formulas? Keep reading our blogs to learn more about the Basic Concepts of Maths!