One app for all your study abroad needs
Cylinders are three-dimensional shapes with real-world uses such as soup cans and pipes. Moreover, understanding the surface area of a cylinder is required for different purposes. One example would be estimating the paint needed or calculating the material required to create a cylindrical object. Additionally, this blog tells you about the concept of the Curved Surface Area of a Cylinder, the formula and examples.
Also Read: Surface Areas and Volumes
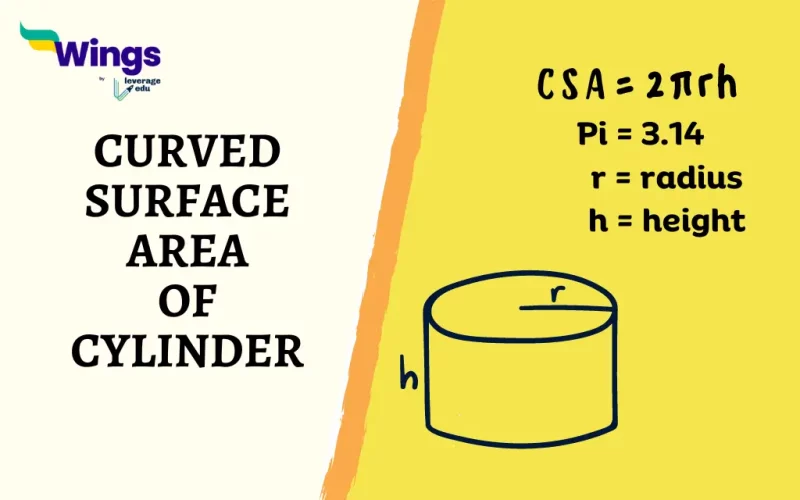
What is the Formula for the Curved Surface Area of a Cylinder?
If you unroll the Curved surface of a cylinder it will change into a flat rectangle. Additionally, the length of this rectangle is equal to the cylinder’s circumference, which is 2πr (where r is the base radius and π is pi). Moreover, the height of the rectangle stays the same as the cylinder’s height (h).
Therefore, the formula for the Curved surface area of a cylinder (CSA) is:
CSA = 2πrh
Here,
- CSA represents the Curved surface area.
- π (pi) is a mathematical constant with an approximate value of 3.14.
- r represents the base radius of the cylinder.
- h represents the height of the cylinder.
Also Read: 20+ Volume and Surface Area Questions and Answers
Curved Surface Area of Cylinder Example
Let us say you have a tin can with a base radius of 5 centimetres and a height of 10 centimetres. You want to find the Curved surface area (the area excluding the top and bottom circles) needed to wrap a creative label around the can.
Using the formula CSA = 2πrh:
- CSA = 2 ✕ 3.14 ✕ 5 ✕ 10 (assuming the value of π as 3.14)
- CSA = 314 cm²
Thus, you will need approximately 314 square centimetres of material for your creative label.
Take a look at another example. The radius is 3 meters and the height is 8 meters. Again we shall take the Formula, CSA = 2πrh.
- 2 ✕ 3.14 ✕ 3 ✕ 8 (assuming the value of π as 3.14)
- CSA = 150 m²
Therefore, with the radius being 3 meters and the height being 8 meters, the CSA is 150 m².
Related Blogs
I hope this helps! Did you like learning about the Curved Surface Area of Cylinder? Keep reading our blogs to learn more about the basic concepts of Maths!