Harmonic Mean Formula: Definition, Examples, and Applications

The harmonic mean (HM)is one of the several types of numerical averages, particularly categorized as a Pythagorean mean alongside the arithmetic mean (AM) and geometric mean (GM). These three means are valuable in various fields, including geometry and music. In the context of a data set, the HM can be conceptualized as the reciprocal of the arithmetic mean of the reciprocals within the data. In other words, it represents the inverse of the average speed obtained by taking reciprocals of individual speeds. This property makes HM particularly useful for calculating average rates or rates of change.

What is Harmonic Mean?

The harmonic mean (HM) contributes as one of several central tendency measures used in statistics to summarize a data set’s behaviour around a central point. Alongside the more familiar mean, median, and mode, the harmonic mean falls under the umbrella of “mean” itself, further categorized alongside arithmetic and geometric means. 

Central tendency measures tries to capture a single, representative value within the data. The harmonic mean achieves this by considering the reciprocals of each data point. This focus on reciprocals makes it particularly suitable for averaging rates or rates of change, as it grants greater influence to smaller values within the data set.Here is the formula representing harmonic mean:

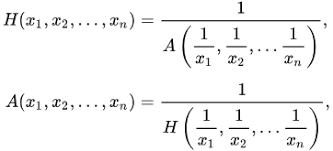
Definition of Harmonic Mean

The harmonic mean is a unique average standard for calculating rates. It prioritizes smaller values within a data set. Unlike the arithmetic or geometric mean, it’s calculated by dividing the number of terms by the sum of their reciprocals. This makes it the lowest value among the three Pythagorean means.

Example to Explain Harmonic Mean Formula

Let’s deal with the harmonic mean of the sequence 1, 3, 5, 7. Since it’s an arithmetic progression, the reciprocals (1, 1/3, 1/5, 1/7) also form a harmonic progression. The harmonic mean itself is calculated by dividing the number of terms (4 in this case) by the sum of their reciprocals (which we need to find). It’s like averaging the speeds (reciprocals) instead of the values themselves.  Adding the reciprocals (1 + 1/3 + 1/5 + 1/7), we get approximately 1.9286. Dividing 4 by this value, the harmonic mean of the sequence is roughly 2.07.

How to Find Harmonic Mean?

Here’s how to find the harmonic mean in easy steps:

1. Take the reciprocal (flip it upside down) of each number in your data set.
2. Figure out how many numbers you have (total number of terms).
3. Add up all the reciprocals you calculated in step 1.
4. Divide the number you got in step 2 (total terms) by the sum you got in step 3 (sum of reciprocals).

Harmonic Mean Vs Geometric Mean

Here in this section we have listed the important differences between harmonic mean and geometric mean in great detail:

Measure of Central Tendency	Harmonic Mean	Geometric Mean
Calculation method	Divide the total number of terms by the sum of their reciprocals.	Multiply all terms and take the nth root, where n is the number of terms.
Value comparison	Always less than other two means.	Always greater than harmonic mean but less than arithmetic mean.
Interpretation	It’s like finding the average after certain reciprocal transformations.	Think of it as the average with certain log transformations.
Example	Given: 1, 2, 4, 7. Harmonic Mean = 4 / (1/1 + 1/2 + 1/4 + 1/7) = 2.113	Given: 1, 2, 4, 7. Geometric Mean = (1 × 2 × 4 × 7)^(1/4) = 2.735

Harmonic Mean vs Arithmetic Mean

Here in this section, we have listed the important differences between harmonic mean and arithmetic mean in great detail:

Aspect	Harmonic Mean	Arithmetic Mean
Calculation Method	Take the reciprocal of the arithmetic mean of the reciprocal terms in the dataset	Sum of all observations divided by the total number of observations
Relative Magnitude	Lowest value among the three Pythagorean means	Highest value among the three Pythagorean means
Applicability	Cannot be used on a dataset consisting of negative or zero values	Can be calculated for datasets with negative, positive, and zero values
Example Calculation	Given dataset: 3, 2, 1, 6<br>Harmonic Mean = 4 / (1/3 + 1/2 + 1/1 + 1/6) = 2	Given dataset: 3, 2, 1, 6<br>Arithmetic Mean = (3 + 2 + 1 + 6) / 4 = 3

Relation Between AM, GM, and HM

Imagine you have two numbers, like speeds you can travel. There are three ways to find an average that tells you something about those speeds:

• Regular average (arithmetic mean): Add the speeds and divide by two. This is good if the speeds are just numbers you want to combine.
• Geometric mean: This is like an average that considers rates of change. Imagine multiplying the speeds together, then taking the square root. This is useful when things multiply over time, like money growing in a bank account.
• Speed average (harmonic mean): This is like an average that considers how fast you go overall. Imagine taking the reciprocal of each speed (like 1 divided by the speed), then averaging those reciprocals, and taking the reciprocal of that result. This is helpful when you’re looking at rates or speeds, because slower speeds will pull the average down more than faster speeds.
• These three averages are related. The speed average (harmonic mean) times the regular average (arithmetic mean) will always be equal to the square of the fancy average (geometric mean).

Merits and Demerits of Harmonic Mean

Some of the merits and demerits of harmonic mean are mentioned in this section:

Merits of Harmonic Mean	Demerits of Harmonic Mean
Based on observations	Requires knowledge of all elements in the series
Rigidly defined	Lengthy and complicated calculation method
Not significantly affected by sample fluctuations	Cannot be calculated if any term in the series is 0
Useful in averaging certain types of rates	Extreme values in the series greatly affect the harmonic mean

Weighted Harmonic Mean

Let’s break down weighted harmonic mean in simpler terms. Imagine you have a bunch of things (like apples) and their sizes (weights).

• Regular Harmonic Mean (for equal importance):
  
  • You want to find an “average size” but give equal weight to EACH apple, no matter how big or small.
  • We take the reciprocal (1 divided by) of each size, then average those reciprocals, and then take the reciprocal of that average to get the harmonic mean (a bit like a weighted average in reverse).
• Weighted Harmonic Mean (with specific weights):
  
  • This is like the regular harmonic mean, but you can give different weights (importance) to each item.
  • Maybe some apples are more important (worth more).
  • The formula considers these weights along with the sizes to find a weighted average size.

FAQs

This was all about the “Harmonic Mean Formula”.  For more such informative blogs, check out our Study Material Section, or you can learn more about us by visiting our  Indian exams page.