Pythagoras Theorem: Proof, Formula, Derivation, Examples  

The Pythagoras theorem is also known as the Pythagorean theorem. It is a basic concept in mathematics that describes the relationship between the lengths of the sides of a right-angled triangle. Furthermore, this theorem is named after the ancient Greek philosopher and mathematician Pythagoras, who is credited with its discovery as well as proof. In addition, the Theorem declares that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Read on to learn more about the father of the Pythagoras Theorem, the Rule for the theorem, the Formula and the Examples along with their solutions. 

Also Read: GRE Geometry: How Important is it?

Who is the Father of the Pythagoras Theorem?

Pythagoras from c. 570 to 495 BCE was a Greek philosopher and mathematician who founded the Pythagorean school in Croton, Italy. 

• He is remembered as one of the most significant mathematicians of all time. 
• Moreover, his contributions to mathematics include the development of the Pythagorean Theorem. 
• Furthermore, Pythagoras was a polymath who made noteworthy contributions to different fields, such as mathematics, music, and philosophy. 
• His teachings emphasised the importance of harmony and balance, which are reflected in the mathematical principles he developed, including the Pythagorean theorem.

Also Read: Conic Sections

What is the Rule for the Pythagorean Theorem?

Additionally, the Pythagorean theorem is a rule that applies specifically to right-angled triangles. Let us see what exactly is the Pythagoras Theorem statement.  

• It states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. 
• This relationship is a fundamental property of right triangles and is used extensively in diverse mathematical and real-world applications.

Also Read: Branches of Mathematics: Arithmetic, Algebra, Geometry, Calculus, Trigonometry, Topology, Probability and Statistics 

Pythagoras Theorem Formula 

Therefore, the Formula for the Pythagoras Theorem is:

c² = a² + b²

where c is the length of the hypotenuse and a and b are the lengths of the other two sides. 

Additionally, this Formula can be used to find the length of the hypotenuse if the lengths of the other two sides are known, or to find the lengths of the other two sides if the length of the hypotenuse is known.

Also Read: Pythagoras Theorem Practice Sheet PDF

Proof of Pythagoras Theorem

Read to find out how you can prove the Pythagoras theorem using simple steps.

1. Let us take a right triangle having points ‘ABC’ with a right angle at point C.
2. a, b, and c are the lengths of sides that are opposite, adjacent, and hypotenuse to the right angle, respectively.
3. Now let us draw squares on each side of the triangle, where side a has points DEFG, side b has points KLMN, and side c has points WXYZ.
4. After that, we will dissect them into smaller squares based on side length.
5. We can rearrange the smaller squares from DEFG and KLMN and find that they can perfectly fill the square WXYZ.
6. Therefore, the area of squares DEFG (a²) and KLMN (b²) combined equals the area of square WXYZ (c²), proving a² + b² = c².

Also Read: Lateral Area of Cylinder: Formula, Example and More! 

Pythagoras Theorem Examples

Moreover, here are some examples of the Pythagoras Theorem:

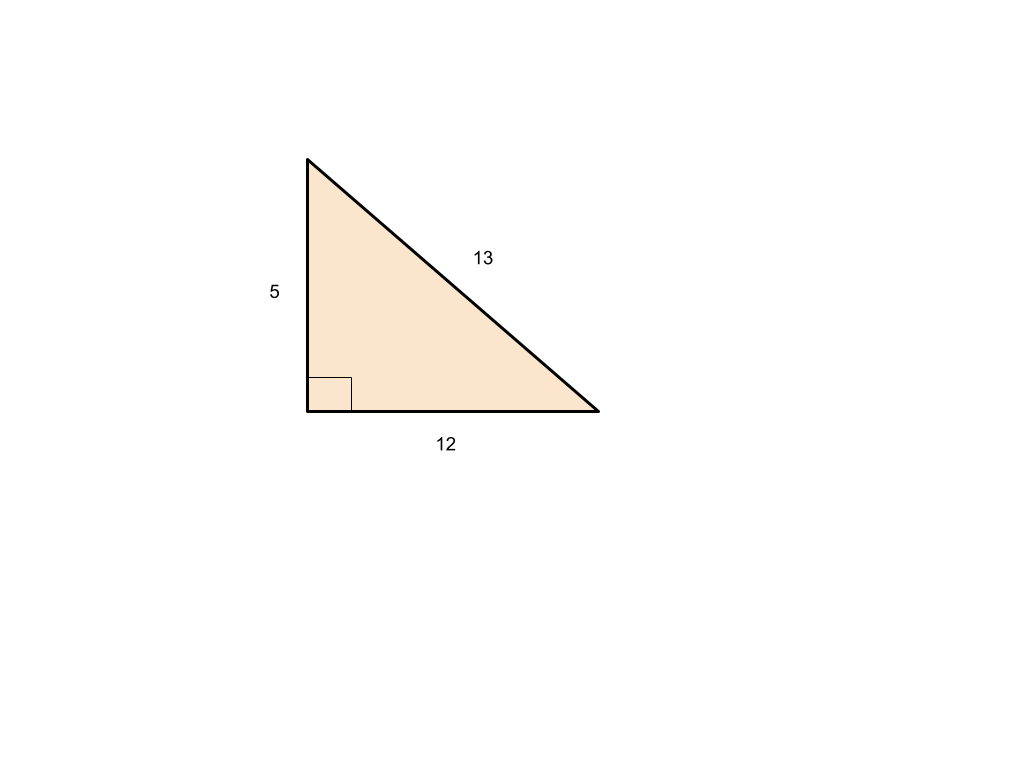
Example 1: Given a triangle with sides 5, 12, and 13 units, applying the Pythagorean Theorem confirms it has a right angle.

Example 2: In a right triangle with sides 7 and 24 units, find the length of the hypotenuse (AC) using the theorem.

Solution 2: Given that the sides of the right triangle are 7 units and 24 units, we can substitute these values into the formula:

c² = 7² + 24²

c² = 49 + 576

c² = 625

Taking the square root of both sides to solve for c (the length of the hypotenuse):

c = √625

c = 25 units

Therefore, the length of the hypotenuse (AC) in the right triangle with sides 7 and 24 units is 25 units.

Also Read: Integration Formulas: Examples and Solutions

Example 3: Calculating the length of the diagonal of a square with a side length of 4 cm using the Pythagorean Theorem.

Solution 3: To calculate the length of the diagonal of a square with a side length of 4 cm using the Pythagorean Theorem, we can apply the formula c = √(a² + b²), where c represents the length of the diagonal, and a and b are the lengths of the sides of the square.

Given that the side length of the square is 4 cm, we can substitute this value into the formula:

c = √(4² + 4²)

c = √(16 + 16)

c = √32

c ≈ 5.65 cm

Therefore, the length of the diagonal of a square with a side length of 4 cm, calculated using the Pythagorean Theorem, is approximately 5.65 cm.

Also Read: Different Types of Angles with Formulas and Examples 

Example 4: Verifying if a triangle with sides 11 cm, 60 cm, and 61 cm forms a right-angled triangle using the theorem.

Solution 4: According to the theorem, in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides.

Given sides:

• Side a = 11 cm
• Side b = 60 cm
• Side c = 61 cm

To verify if this triangle is a right-angled triangle, we can apply the Pythagorean Theorem:

c² = a² + b²

Substitute the given values:

61² = 11² + 60²

3721 = 121 + 3600

3721 = 3721

Since the equation holds true, with 3721 on both sides, the sides 11 cm, 60 cm, and 61 cm form a right-angled triangle. This confirms that the triangle is a right triangle, satisfying the Pythagorean Theorem.

Related Blogs 

7 Types of Fractions with Examples	What are Co Prime Numbers?
How to Find Percentage of Marks?	Multiplication Tables of 1 to 20
Ordinal Numbers from 1 to 100!	Table of 17: Multiples up to 20 & a Trick!
Table of 12: Multiples up to 20!	What is the HCF of Two Consecutive Odd Numbers?

I hope this helps! Did you like learning about the Pythagoras Theorem? Keep reading our blogs to learn more about the Basic Concepts of Maths!