Perimeter of Rhombus: Formula of Side and Diagonals, Examples 

The Perimeter of a shape is the total distance around it. When it comes to a Rhombus all four sides are equal in length. Therefore, the Perimeter of a Rhombus can be acquired by adding all 4 sides or simply multiplying a side into four. Read on to learn more about the Perimeter of a Rhombus, the Formula to find the Perimeter of a Rhombus when the Sides and Diagonals are given in the question and Examples of the same. 

What is a Rhombus?

A Rhombus is a four-sided shape which is also called a quadrilateral where all four sides have the same length. Imagine the shape of a Diamond.  

Furthermore, here are Points to Remember about a Rhombus:

• All sides of a Rhombus have equal lengths.

• Corresponding angles located on opposite sides are of equal measure.

• The opposite sides run parallel to each other.

• The total sum of any two neighbouring angles equals 180 degrees.

• Each diagonal divides the vertex angles into two equal parts.

• The diagonals intersect each other at right angles, hence dividing each other into equal parts.

Also Read: 30 + Square Root and Cube Root Questions and Answers

Perimeter of a Rhombus Formula when Sides are given 

When the Sides of a Rhombus are given, the Formula is simple. As you are already aware the sides of a Rhombus are equal. Hence, to find out the Perimeter of a Rhombus you need to add up all the sides. 

Perimeter = a + a + a + a 

Or 

Perimeter = 4 a (which means a is multiplied 4 times)

For Example, if the side given is 4 meters. Thus, the Perimeter shall be:

Perimeter = 4 + 4 + 4 + 4 = 16 

Or 

Perimeter = 4 ✕ 4 = 16 

Therefore, the Perimeter of a Rhombus whose side is 4 meters is 16. 

Also Read: Perfect Squares: Concepts, Properties & GMAT Questions

Perimeter of a Rhombus Formula when Diagonals are given 

A Rhombus has two diagonals that intersect with each other at Right angles = 90 degrees. Additionally, these Diagonals split the Rhombus into four right-angled triangles. The Diagonals of a Rhombus also bisect each other which means that they cut each other in half.

Things to keep in mind:

• When the Diagonals intersect, they create right-angled triangles inside the Rhombus.

• Moreover, each side of the Rhombus is the hypotenuse of these right-angled triangles.

• To find the side length of the Rhombus, you will need to use the Pythagorean theorem (a² + b² = c²) in one of these right-angled triangles.

To keep it simple, follow these steps along with the examples:

• Find the lengths of the diagonals.
  • Suppose the lengths of the diagonals are 5 and 10. 

• Square both lengths and add them together.
  • 5²  = 25
  • 10² = 100

25 + 100 = 125

• Take the Square root of that sum.
  • Square Root of 125 = 11.18

• Multiply by 2 to get the Perimeter.
  • 11.18 ✕ 2 = 22.36

Thus, the Perimeter of the Diagonals 5 and 10 is 22.36

Also Read: Top 10 Short Maths Tricks for Complex Problems

What is the Perimeter of Rhombus with Diagonals 10 and 24?

The Perimeter of Rhombus with Diagonals 10 and 24 is as follows:

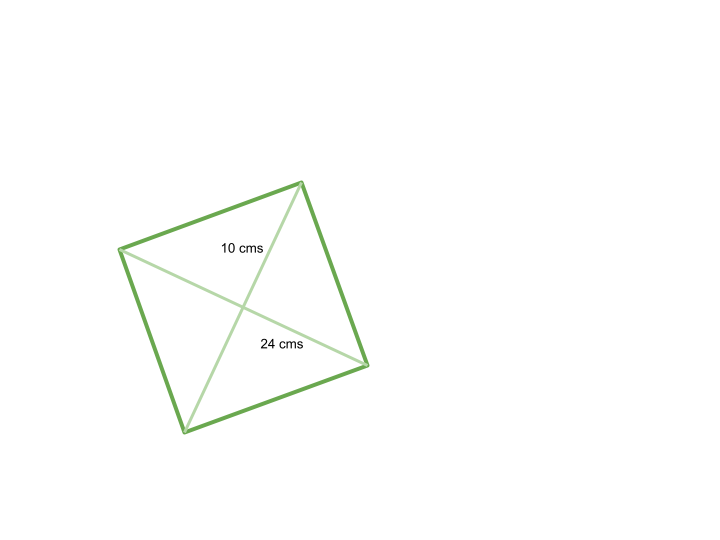
10 = 10² = 100

24 = 24² = 576

100 + 576 = 676

The Square root of 676 = 26

26 ✕ 2 = 52

Thus, the Perimeter of Rhombus with Diagonals 10 and 24 is 52. 

Related Blogs 

7 Types of Fractions with Examples	Factors of 25
Factors of 20	Multiplication Tables of 1 to 20
Ordinal Numbers from 1 to 100!	Table of 17: Multiples up to 20 & a Trick!
Table of 12: Multiples up to 20!	Formula of Profit and Loss

I hope this helps! Did you like learning about the Perimeter of Rhombus? Also, keep reading our blogs to learn more about the Basic Concepts of Maths!