One app for all your study abroad needs
Answer
Verified
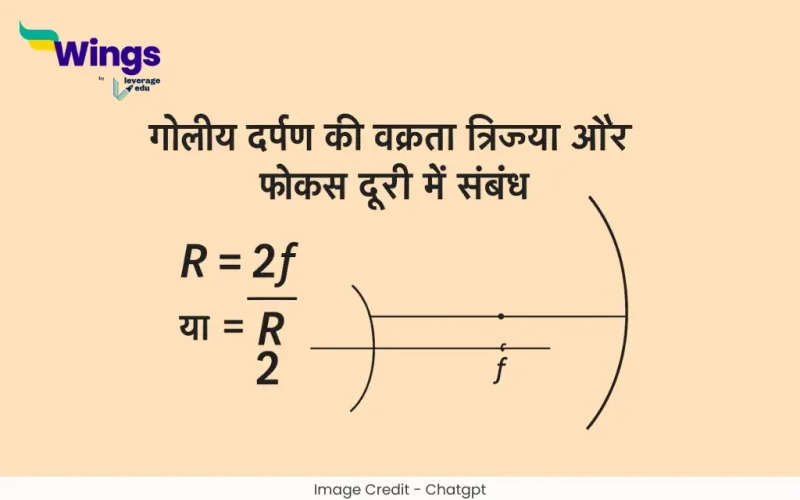
उत्तर: गोलीय दर्पण (Spherical Mirror), चाहे वह अवतल हो या उत्तल, उसकी वक्रता त्रिज्या (Radius of Curvature – R) और फोकस दूरी (Focal Length – f) के बीच एक स्पष्ट और महत्वपूर्ण गणितीय संबंध होता है:
| R = 2f या f = R/2 |
इसका अर्थ है कि—
- दर्पण की वक्रता त्रिज्या उसकी फोकस दूरी की दो गुनी होती है।
- और फोकस दूरी वक्रता त्रिज्या की आधी होती है।
इसका कारण यह है:
जब कोई प्रकाश किरण मुख्य अक्ष (Principal Axis) के समानांतर किसी गोलीय दर्पण पर गिरती है, तो वह परावर्तित होकर फोकस बिंदु (Focus Point) से होकर गुजरती है। यह फोकस बिंदु हमेशा दर्पण के ध्रुव (Pole) और वक्रता केंद्र (Centre of Curvature) के बीच स्थित होता है। इसी कारण फोकस दूरी, वक्रता त्रिज्या का आधा होती है।
महत्वपूर्ण तथ्य:
- यह नियम तभी सही माना जाता है जब दर्पण का मुड़ा हुआ भाग बहुत छोटा हो, जिसे ‘छोटा द्वारक’ (Small Aperture)’ कहते हैं।
- यह संबंध प्रकाशिकी (Optics) में दर्पणों द्वारा बनने वाले प्रतिबिंबों (Images) को समझने में अत्यंत सहायक होता है।
यह भी पढ़ें :
60,000+ students trusted us with their dreams. Take the first step today!