Different Types of Angles with Formulas and Examples 

If you ever get a chance to look around you there are so many Types of Angles that you might notice. Moreover, from a closed door to a sharpened pencil to our Earth’s axis, they all have Angles. However, differentiating between all of them might seem like a task. But in this blog, you will learn about all the 15 Types of Angles along with their formulas as well as examples to help you differentiate. 

Also Read: What is the Difference Between Degrees and Radians?

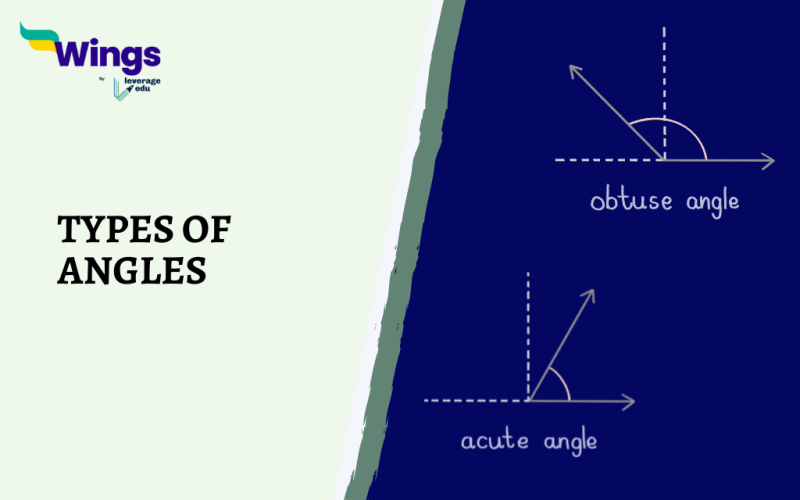
Acute Angle

An Acute angle is an angle that measures less than 90 degrees.

The Formula for an Acute angle is: Acute Angle = x°, where 0° < x < 90°

Example: An angle of 45 degrees is an Acute angle or the corner of a sharpened pencil.

Right Angle

A Right angle is an angle that measures exactly 90 degrees. 

The Formula for a Right angle is: Right Angle = 90°

Example: The angle formed by the intersection of two perpendicular lines is a Right angle or a closed door.

Here the Right Angle is ABC and AGD. 

Obtuse Angle

An Obtuse angle is an angle that measures more than 90 degrees but less than 180 degrees.

The Formula for an Obtuse angle is: Obtuse Angle = x°, where 90° < x < 180°

Example: An angle of 135 degrees is an Obtuse angle or a leaning tree. 

Straight Angle

A Straight angle is an angle that measures exactly 180 degrees. 

The Formula for a Straight angle is: Straight Angle = 180°

Example: The angle formed by a line segment that extends in a Straight line is a straight angle. 

Reflex Angle

A Reflex angle is an angle that measures more than 180 degrees but less than 360 degrees. 

The Formula for a Reflex angle is: Reflex Angle = x°, where 180° < x < 360°

Example: An angle of 225 degrees is a Reflex angle or the hands of a clock forming a “V” shape.

Full Rotation Angle

A Full Rotation angle is an angle that measures exactly 360 degrees. 

The Formula for a Full Rotation angle is: Full Rotation Angle = 360°

Example: The angle formed by a complete revolution around a circle is a Full Rotation angle or the Earth’s rotation on its axis.

Positive Angles

Positive angles are angles that are measured in a counterclockwise direction from the positive x-axis. 

The Formula for a Positive angle is: Positive Angle = x°, where 0° ≤ x < 360°

Example: An angle of 45 degrees measured in a counterclockwise direction from the positive x-axis is a Positive angle. Moreover, any Acute, Obtuse, or Reflex angle.

Negative Angles 

Negative angles are angles that are measured in a clockwise direction from the positive x-axis. 

The Formula for a Negative angle is: Negative Angle = -x°, where -360° < x ≤ 0°

Example: An angle of -45 degrees measured in a clockwise direction from the positive x-axis is a Negative angle. 

Adjacent Angles

Adjacent angles are two angles that share a common vertex and a common side. The sum of the measures of Adjacent angles is always 180 degrees. 

The Formula for Adjacent angles is: Adjacent Angles = x° + y°, where x° + y° = 180°

Example: The two angles formed by the intersection of two perpendicular lines are Adjacent angles.

Complementary Angles

Complementary angles are two angles whose sum is exactly 90 degrees. 

The Formula for Complementary angles is: Complementary Angles = x° + y°, where x° + y° = 90°

Example: An angle of 25 degrees and an angle of 65 degrees are Complementary angles or two Acute angles on a perpendicular line.

Supplementary Angles

Supplementary angles are two angles whose sum is exactly 180 degrees. 

The Formula for Supplementary angles is: Supplementary Angles = x° + y°, where x° + y° = 180°

Example: An angle of 120 degrees and an angle of 60 degrees are Supplementary angles or two Straight angles next to each other.

Alternate Interior Angles

Alternate Interior angles are two angles that are on opposite sides of a transversal line and are on the interior of the two parallel lines. 

The Formula for Alternate Interior angles is: Alternate Interior Angles = x°, where x° = y°

Example: The angles formed by a transversal line intersecting two parallel lines are Alternate Interior angles.

Alternate Exterior Angles

Alternate Exterior angles are two angles that are on opposite sides of a transversal line and are on the exterior of the two parallel lines. 

The Formula for Alternate Exterior angles is: Alternate Exterior Angles = x°, where x° = y°

Example: The angles formed by a transversal line intersecting two parallel lines, but on the exterior of the parallel lines, are Alternate Exterior angles.

Here AGE and DOF are Alternate exterior angles.

Corresponding Angles

Corresponding angles are two angles that are on the same side of a transversal line and are on the same side of the two parallel lines. 

The Formula for Corresponding angles is: Corresponding Angles = x°, where x° = y°

Example: The angles formed by a transversal line intersecting two parallel lines, where the angles are on the same side of the transversal line, are Corresponding angles.

Vertical Angles

Vertical angles are two angles that are opposite each other when two lines intersect. 

The Formula for Vertical angles is: Vertical Angles = x°, where x° = y°

Example: The angles formed by the intersection of two lines are Vertical angles.

Maths Problems on Angles with Solutions

1. An angle measures 120 degrees. What type of angle is it?
   Answer: Obtuse angle (An obtuse angle has a measure greater than 90° but less than 180°).
2. Line m intersects line n at point O. If angle 1 measures 45 degrees, what is the measure of its complementary angle?
   Answer: 45 degrees (Since they are complementary, the other angle must also measure 45 degrees to reach 90 degrees).
3. Two rays, OA and OB, lie on a straight line. What is the measure of angle AOB?
   Answer: 180 degrees (A straight line creates an angle of 180 degrees).
4. The angles in a triangle add up to 180 degrees. If one angle in a triangle measures 60 degrees and another measures 70 degrees, what type of angle is the third angle?
   Answer: Acute angle (The third angle must be less than 50 degrees (180 – 60 – 70) to fit within the triangle).
5. At what time on an analog clock do the hour and minute hands form a right angle (90 degrees)?
   Answer: 3:00 (The hour hand moves 360 degrees in 12 hours, so it moves 30 degrees every hour.)

Related Blogs 

7 Types of Fractions with Examples	What are Co Prime Numbers?
How to Find Percentage of Marks?	Multiplication Tables of 1 to 20
Ordinal Numbers from 1 to 100!	Table of 17: Multiples up to 20 & a Trick!
Table of 12: Multiples up to 20!	What is the HCF of Two Consecutive Odd Numbers?

I hope this helps! Did you like learning about Types of Angles? Keep reading our blogs to learn more about the basic concepts of Maths!