One of the biggest differences between uniform and Non-Uniform motion lies in how an object’s speed changes over time. In uniform motion, an object travels in a straight line with constant speed and covers the same distance in the same amount of time. It means the object maintains a constant speed without any changes in its speed. In Non-Uniform motion, the object’s speed changes over time.
As a result, the object covers different distances in the same amount of time. It change in speed can involve acceleration, which is known as speeding up, deceleration, which is known as slowing down, or changes in direction.
Table of Contents [show]
What is Uniform Motion?
Uniform motion refers to the movement of an object in a straight line with a constant velocity (speed). Here’s a breakdown of key points of uniform motion.
- Constant Velocity: The object moves at a steady speed, maintaining the same magnitude (value) of velocity.
- Straight Line Path: The object travels in a straight line without deviating from its path.
- Equal Displacement in Equal Intervals: The object covers equal distances in equal intervals of time. This means that if you measure the distance the object travels over fixed time intervals (like every second), you will find that the distances are the same.
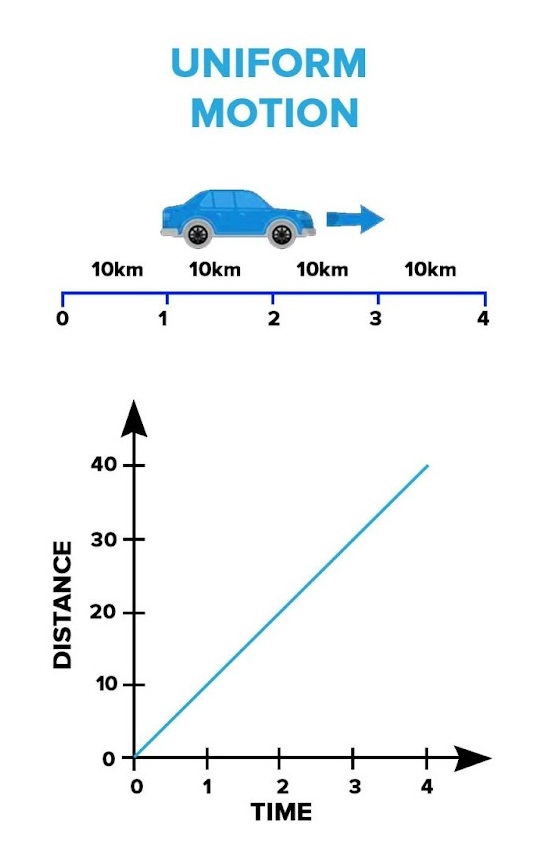
Uniform motion is characterized by a consistent and unchanging rate of movement. Here are some real-world examples of uniform motion.
- A car cruising on a highway at a constant speed.
- An airplane travels at a constant altitude and speed in a straight line.
- A train moving on a straight track at a steady velocity.
What is Non-Uniform Motion?
The non-uniform motion describes the movement of an object where its speed and or direction change over time. Unlike uniform motion with its constant characteristics, non-uniform motion is all about variation. Here’s a breakdown of key points and features of non-uniform motion.
- Changing Velocity: The object’s speed (magnitude of velocity) or direction (or both) varies as time progresses.
- Unequal Displacement in Equal Intervals: Unlike uniform motion, where equal intervals of time result in equal displacements, in non-uniform motion, equal time intervals yield different displacements.
- Acceleration or Deceleration: Non-uniform motion often involves acceleration (increase in speed), deceleration (decrease in speed), or changes in direction.
- Distance vs Time Graph: The path of a non-uniformly moving object on a distance vs time graph won’t be a straight line, but rather a curve.
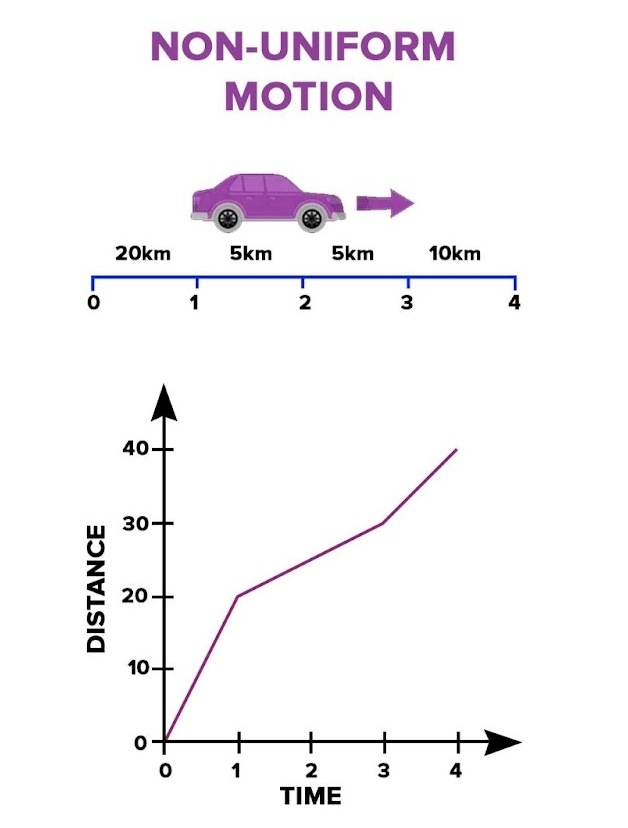
Here are some everyday examples of non-uniform motion.
- A car coming to a stop at a red light (decelerating).
- A swinging pendulum (speed changes throughout the swing).
- A ball is thrown upwards (starts with a certain speed, slows down due to gravity, then speeds down again as it falls).
- A race car going around a curved track (changes both speed and direction).
Also Read: 20+ Questions of Cause and Effect Reasoning
Difference Between Uniform and Non-Uniform Motion
Here’s a comparison between uniform and non-uniform motion that is mentioned below.
| Characteristics | Uniform Motion | Non-Uniform Motion |
| Velocity | Constant | Changes over time |
| Path | Straight line | Can be curved or straight |
| Displacement | Equal displacements in equal time intervals | Unequal displacements in equal time intervals |
| Acceleration | No acceleration or deceleration | Acceleration, deceleration, or change |
| Example | Car moving at a constant speed on a straight road | Car accelerating from rest, ball thrown upwards |
Uniform and Non-Uniform Motion Formulas
In uniform motion, the object’s speed (and therefore velocity) remains constant. Here are some useful formulas to analyze this type of motion.
For Uniform Motion
| Distance (d) = v x t |
Where:
- d = distance traveled (meters, kilometers, etc.)
- v = constant speed (meters per second, kilometers per hour, etc.)
- t = time interval (seconds, hours, etc.)
| Average Speed (s) = D (Total Distance) / T (Total Time Taken) |
where:
- D = Total Distance traveled by object
- T = Total time taken by object
Relationship between Speed and Time
| t = d / v |
Where:
- t = Time
- d = Distance
- v = Speed
For Non-Uniform Motion
Average Speed (s)
| Average Speed(s) = Total distance / Total time taken |
Acceleration (a)
| Acceleration (a) = (Final Velocity(V) – Initial Velocity(v)) / t |
Where:
- a = acceleration (meters per second squared, kilometers per hour squared, etc.)
- V = final speed
- v = initial speed
- t = time interval
Similarities Between Uniform and Non-Uniform Speed
Uniform and non-uniform speeds are both ways of describing how fast something is moving, but they differ in how consistent that speed is.Both are measured in speed units: We use units like kilometers per hour (kph) or miles per hour (mph) for both uniform and non-uniform speeds.They might be different speeds, but they’re measured in the same way.
20+ Sample Q&A of Uniform and Non-Uniform Motion
Q1. A car travels at a constant speed of 60 km/h. How far will it travel in 2 hours?
Solution: Distance = Speed × Time Distance = 60 km/h × 2 h = 120 km.
Q2. A car accelerates from rest at a rate of 2 m/s² for 5 seconds. How far does it travel during this time?
Solution: Using the equation for distance traveled under constant acceleration: Distance = Initial velocity × Time + 0.5 × Acceleration × Time² Distance = 0 m/s × 5 s + 0.5 × 2 m/s² × (5 s)² Distance = 0 + 0.5 × 2 m/s² × 25 s² = 25 m.
Q3. A train travels at a constant speed of 80 km/h. How long will it take to travel 400 km?
Solution: Time = Distance / Speed Time = 400 km / 80 km/h = 5 hours.
Q4. An object starts from rest and accelerates uniformly at 3 m/s² for 4 seconds. What is its final velocity?
Solution: Final velocity = Initial velocity + Acceleration × Time Initial velocity = 0 m/s Final velocity = 0 m/s + 3 m/s² × 4 s = 12 m/s.
Q5. A cyclist rides at a constant speed of 15 km/h. How far does she travel in 3 hours?
Solution: Distance = Speed × Time Distance = 15 km/h × 3 h = 45 km.
Q6. A rocket starts from rest and accelerates uniformly at 10 m/s² for 8 seconds. What is its final velocity?
Solution: Final velocity = Initial velocity + Acceleration × Time Initial velocity = 0 m/s Final velocity = 0 m/s + 10 m/s² × 8 s = 80 m/s.
Q7. A bus travels at a constant speed of 50 mph. How long does it take to travel 200 miles?
Solution: Time = Distance / Speed Time = 200 miles / 50 mph = 4 hours.
Q8. An object starts from rest and accelerates uniformly at 5 m/s² for 6 seconds. What distance does it cover during this time?
Solution: Using the equation for distance traveled under constant acceleration: Distance = Initial velocity × Time + 0.5 × Acceleration × Time² Distance = 0 m/s × 6 s + 0.5 × 5 m/s² × (6 s)² Distance = 0 + 0.5 × 5 m/s² × 36 s² = 90 m.
Q9. A boat travels at a constant speed of 25 knots. How far does it travel in 6 hours?
Solution: Distance = Speed × Time Distance = 25 knots × 6 hours = 150 nautical miles.
Q10. A car decelerates uniformly from 30 m/s to 10 m/s in 5 seconds. What is its deceleration?
Solution: Deceleration = (Final Velocity – Initial Velocity) / Time Deceleration = (10 m/s – 30 m/s) / 5 s = -4 m/s².
Q11. A plane flies at a constant speed of 600 mph. How long will it take to travel 3000 miles?
Solution: Time = Distance / Speed Time = 3000 miles / 600 mph = 5 hours.
Q12. A ball is thrown upwards with an initial velocity of 20 m/s. How long does it take to reach its maximum height?
Solution: Use the equation: Final velocity = Initial velocity + Acceleration × Time At maximum height, final velocity becomes 0 m/s. 0 m/s = 20 m/s – 9.8 m/s² × Time (as acceleration due to gravity acts downwards) Time = 20 m/s / 9.8 m/s² = 2.04 seconds.
Q13. A runner runs at a constant speed of 10 m/s. How far does he travel in 30 seconds?
Solution: Distance = Speed × Time Distance = 10 m/s × 30 s = 300 meters.
Q14. A car accelerates from 20 m/s to 40 m/s in 5 seconds. What is its acceleration?
Solution: Acceleration = (Final Velocity – Initial Velocity) / Time Acceleration = (40 m/s – 20 m/s) / 5 s = 4 m/s².
Q15. A train moves at a constant speed of 80 km/h. How far will it travel in 2.5 hours?
Solution: Distance = Speed × Time Distance = 80 km/h × 2.5 h = 200 km.
Q16. A car accelerates uniformly from 5 m/s to 20 m/s in 10 seconds. What is its acceleration?
Solution: Acceleration = (Final Velocity – Initial Velocity) / Time Acceleration = (20 m/s – 5 m/s) / 10 s = 1.5 m/s².
Q17. A cyclist rides at a constant speed of 25 km/h. How long will it take to travel 50 kilometers?
Solution: Time = Distance / Speed Time = 50 km / 25 km/h = 2 hours.
Q18. A car decelerates uniformly from 25 m/s to 10 m/s in 4 seconds. What distance does it cover during this time?
Solution: Using the equation for distance traveled under constant acceleration: Distance = Initial velocity × Time – 0.5 × Acceleration × Time² Distance = 25 m/s × 4 s – 0.5 × (25 m/s²) × (4 s)² Distance = 100 m – 0.5 × 25 m/s² × 16 s² = 100 m – 200 m = -100 m The negative sign indicates that the car moves in the opposite direction.
Q19. A boat travels at a constant speed of 15 knots. How far does it travel in 4 hours?
Solution: Distance = Speed × Time Distance = 15 knots × 4 hours = 60 nautical miles.
Q20. A rocket starts from rest and accelerates uniformly at 20 m/s² for 5 seconds. What is its final velocity?
Solution: Final velocity = Initial velocity + Acceleration × Time Initial velocity = 0 m/s Final velocity = 0 m/s + 20 m/s² × 5 s = 100 m/s.
Also Read: 20+ Questions of Arithmetic Reasoning
FAQ’s
When there is uniform motion, the speed doesn’t change. When an object’s speed changes over time, this is called non-uniform motion.
A car going at a steady speed of 10 meters per second will go the same distance every second, so its motion will be smooth. It doesn’t matter how small the time gaps are; if a person moves uneven lengths in similar amounts of time, that motion is called non-uniform.
It can be represented as A = (Vf – Vi) / t, where A is acceleration, Vf is final velocity, Vi is initial velocity and t is the time interval.
RELATED BLOGS
This was all about the “Difference between Uniform and Non-Uniform Motion”. For more such informative blogs, check out our Study Material Section, you can learn more about us by visiting our Indian exams page.
 One app for all your study abroad needs
One app for all your study abroad needs















 45,000+ students trusted us with their dreams. Take the first step today!
45,000+ students trusted us with their dreams. Take the first step today!
