Every rational number is ____

Answer: Every rational number is a real number. Thus, the correct option is C.

Complete Answer:

Every rational number is a real number because it can be written as a fraction or ratio of two integers, where the denominator is not zero. In simple terms, any number that can be expressed in the form p/q, where p and q are integers and q ≠ 0, is a rational number. 

For example, numbers like 3/4, -2, 5, and 0 are all rational because they can be written in fractional form.

What is the Real Number System?

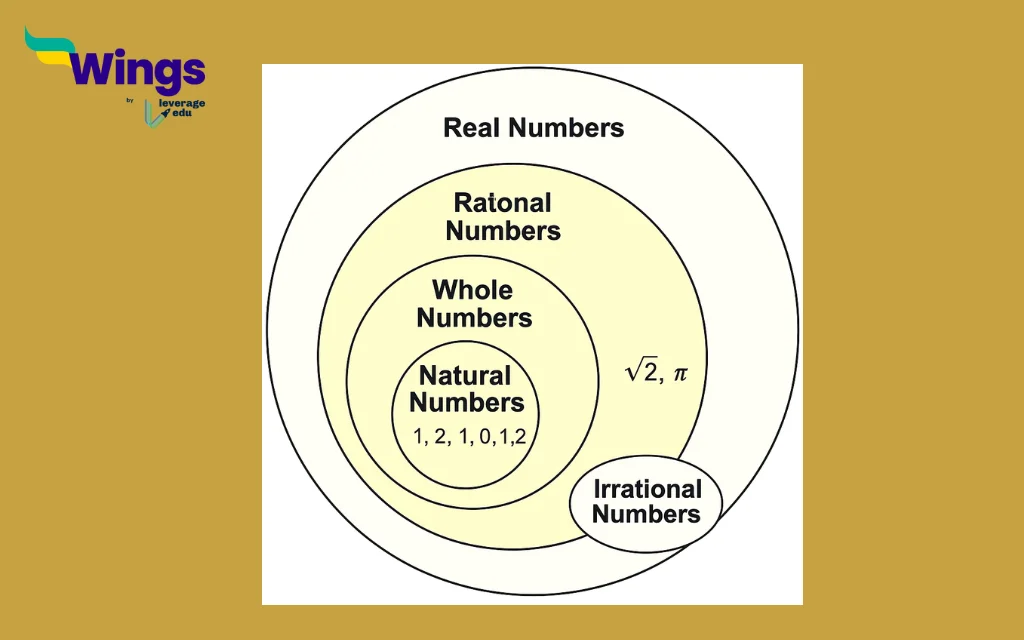
The real number system includes all the numbers that can be found on the real number line. It consists of two main categories: rational numbers and irrational numbers. While irrational numbers (like √2 or π) cannot be written as exact fractions, rational numbers can always be written in fraction form. This makes every rational number a part of the real number system.

Let us look at the other options to understand why they are incorrect.

(a) A natural number:

Natural numbers are positive counting numbers like 1, 2, 3, and so on. Rational numbers include not only positive numbers but also zero, negative numbers, and fractions. 

For instance, -3 and 2/7 are rational but not natural. Therefore, every rational number is not a natural number.

(b) An integer:

Integers are whole numbers that can be positive, negative, or zero, such as -4, 0, or 6. While integers are rational numbers, not all rational numbers are integers. 

For example, 5/3 is a rational number but not an integer. So, every rational number is not an integer.

(d) A whole number:

Whole numbers are the numbers which include all natural numbers and zero (0, 1, 2, 3,…). Again, rational numbers such as fractions and negative numbers do not fit into this group. 

For example, -1 and 3/4 are rational but not whole numbers.

Interesting Fact About Rational Numbers

Every rational number is a real number, but not every real number is rational. Rational numbers have repeating or terminating decimals, while real numbers also include irrationals like √2 and π, which have endless, non-repeating decimal expansions.

Check out other Mathematics questions from here:

Find the mean of the first 10 even natural numbers	The average of the least and the greatest prime number of 2 digits is
The only even prime number is	Find Twin Prime Numbers Between 100 and 200
The instrument in the geometry box in the shape of a triangle is called a	Using Empirical Formula Calculate the Mode of the Following Data: 17, 16, 25, 23, 22, 23, 28, 25, 25, 23.