Question: Find the Arithmetic Mean of the Progression 2, 4, 6, 8, 10

Correct Option: D. 6 

Identifying an arithmetic progression is important for mastering sequences. The above given progression  2, 4, 6, 8, 10 can be seen by calculating the mean by summing all terms and dividing by the number of terms, which results in 6. The outcome showcases the midpoint property of evenly spaced data and emphasizes the elegance of arithmetic sequences in algebra. As an 11th-class student, if you want to know how to calculate the answer, you can read this article. Keep in mind that the answer to the question -Find the arithmetic mean of the progression 2, 4, 6, 8, 10 is  6 (Option D)

Recognize the sequence

The above terms are from an arithmetic progression with a constant difference d=2d = 2. It has to be kept in mind that in an arithmetic sequence every term increases by the same amount ‘d’ between successive terms.

Sum of the progression

For the above arithmetic progression of n terms. The total of Sns_n can be identified  by:

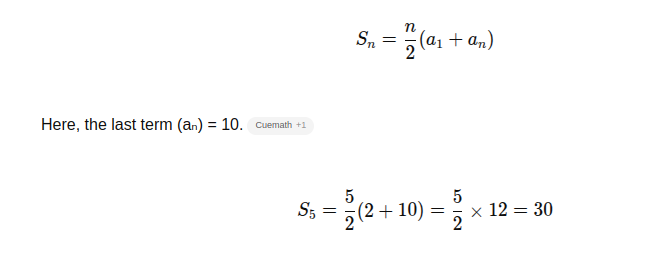
Compute the Arithmetic Mean

The total divided by the count is the arithmetic mean, or average, of n numbers

Alternative shortcut

The mean can also be found by averaging the first and last terms:

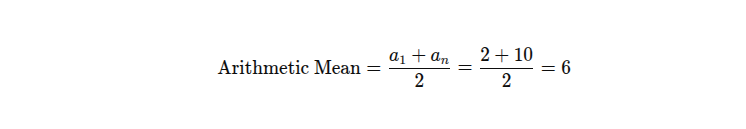
This shortcut helps in saving computation by using the symmetry of equally spaced terms. 

Learning about the arithmetic mean within an arithmetic progression ties together the series, the sequences, and statistics. Identifying that the mean of evenly spaced data points is the midpoint emphasises algebraic fluency and data interpretation skills. Applying this idea can help in solving more such problems consisting of weighted averages, statistical distributions, and real-world modelling.

Related Articles:

Find 25% of What Number Gives 9?	Find Twin Prime Numbers Between 100 and 200
The Number of Corners in a Cylinder is__	How Many Numbers of Two Digit are Divisible by 3?
How Many Squares Are There in a Chess Board?	How do you split the middle term in quadratic equations?