What is the Difference Between Covariance and Correlation?

The difference between covariance and correlation is that correlation assesses the strength and direction of the linear link between two variables, while covariance just shows the direction of the relationship. So, the covariance determines the correlation.

What is Covariance?

Covariance is the measure of changes between two random variables in statistics. This table provides an overview of covariance, covering its definition, calculation, importance, relationship with risk, types, and differences from correlation.

Definition	Covariance measures the directional relationship between returns on two assets. Positive means they move together, and negative means they move inversely.
Calculation	Covariance is calculated by analysing return surprises or multiplying correlation by the standard deviations of each variable.
Importance	It’s a tool in modern portfolio theory for diversification, determining securities to include in a portfolio.
Relationship with Risk	Pairing assets with negative covariance helps reduce risk and volatility in a portfolio.
Types	Positive covariance indicates variables move together; negative covariance indicates an inverse relationship.
Difference from Correlation	Covariance measures the direction of the relationship, while correlation measures strength.

Must Read:Difference Between Parallel and Perpendicular

What is Correlation?

A correlation is a statistical measure that indicates the extent to which two or more variables fluctuate concerning each other. This table provides an overview of correlation and its application, including its calculation methods and types.

Definition	Correlation measures the degree to which two or more variables move in sequence. A correlation matrix displays correlation coefficients between variables .
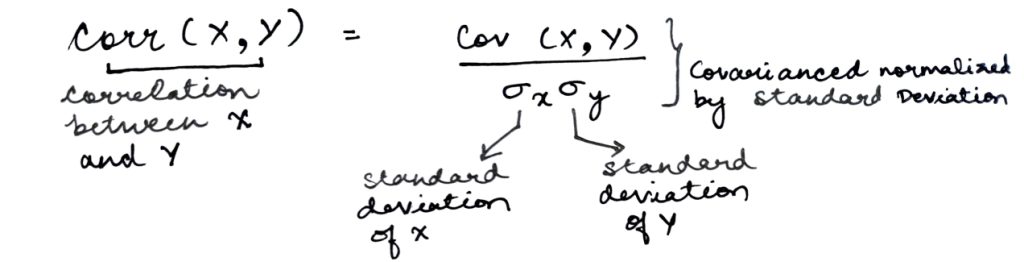
Calculation	The correlation coefficient is calculated by dividing the covariance of two variables by the product of their standard deviations.
Types	Used in data analysis to understand relationships between variables. The correlation matrix helps summarize relationships and guide further analysis.
Application	Used in data analysis to understand relationships between variables. Correlation matrix helps summarize relationships and guide further analysis.
Methods of Calculation	Common methods include coefficient of correlation, rank correlation coefficient, and coefficient of concurrent deviations.

Must Read: Difference Between Marginal Cost and Average Cost

What is the Difference Between Covariance and Correlation

Despite the similarities between these mathematical terms, they are different from each other. Covariance is when two variables vary with each other, whereas correlation is when a change in one variable results in a change in another variable. Here we have differentiated both terms based on the following parameters :

Feature	Covariance	Correlation
Definition	Measures the direction and magnitude of linear dependence between two variables.	Measures the strength and direction of the linear relationship between two variables.
Values	Range: -∞ to +∞	Range: -1 to +1
Change in Scale	Affected by the scale of the data.	Unaffected by the scale of the data (standardised).
Unit-free measure	No	Yes

Covariance and Correlation Formulas 

Covariance explains the joint variability of the variables. This table provides an overview of covariance calculation, interpretation, and its formula:

Covariance Calculation	Covariance is calculated by summing the product of the deviations of returns from their means, then dividing by the sample size minus one.
Example Calculation	Calculate the covariance between two stocks using daily returns over a period. Deviations from means are multiplied and averaged.
Interpretation	Positive covariance suggests similar movements between assets. A covariance of zero indicates no clear directional relationship.
Covariance vs. Variance	Covariance measures the relationship between two variables, while variance measures how closely data points are clustered around the mean in a single variable.
Mathematical Formula	Covariance = Σ [ (Returnabc – Averageabc) * (Returnxyz – Averagexyz) ] ÷ (Sample Size – 1)

Correlation measures the association between the variables. Here we have stated the formula showing its relationship with covariance.

Application of  Covariance and Correlation in Real Life

Covariance and correlation are often used in real life. From finding patterns to diagnosing issues covariance and correlation have numerous advantages to offer:

• Finding patterns: Correlation helps identify relationships between data points. A “correlation matrix” reveals if multiple variables move together (positive correlation) or oppositely (negative correlation). This uncovers hidden trends in large datasets.
• Enabling further analysis: Correlation matrices act as a springboard for other techniques. They feed into methods like factor analysis and regression, which explore deeper connections and make predictions based on the correlations found.
• Diagnosing issues: A correlation matrix can also act as a check. In linear regression, extensive correlations between variables flag potential problems. This helps identify situations where the analysis might be unreliable.

FAQ’s

This was all about the “Difference Between Covariance and Correlation”.  For more such informative blogs, check out our Study Material Section, you can learn more about us by visiting our  Indian exams page.