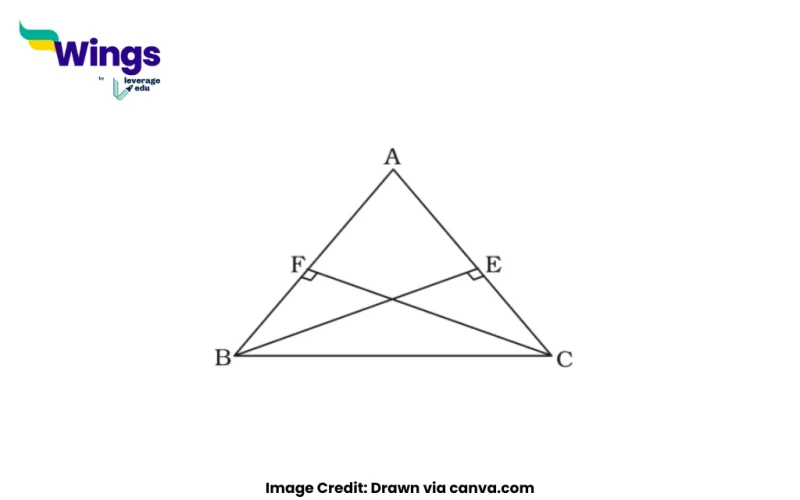
If two altitudes of a triangle are equal in length, prove that it is an isosceles triangle.

If two altitudes of a triangle are equal in length, then the triangle is an isosceles triangle. This can be proved using fundamental geometric principles and properties of altitudes.

Understanding Altitudes in a Triangle

An altitude of a triangle is a perpendicular segment drawn from a vertex to the opposite side (or its extension). Every triangle has three altitudes, which may or may not be of equal length depending on the triangle’s type.

Properties of Altitudes:

• Each altitude is perpendicular to the corresponding base.
• The intersection of all three altitudes is called the orthocenter of the triangle.
• In an isosceles triangle, at least two altitudes are equal.

Given Condition: Two Altitudes Are Equal

Let us consider a triangle ABC, where two of its altitudes are equal in length. Our goal is to prove that this condition implies the triangle is isosceles.

Step-by-Step Proof:

1. Construct Altitudes:
   
   • Let AD and BE be the two equal altitudes in triangle ABC.
   • AD is drawn from A to BC, and BE is drawn from B to AC, both perpendicular to their respective bases.
2. Triangle Properties:
   
   • Since AD = BE, the two right-angled triangles ABD and ABE are formed.
   • Both triangles share the common angle ∠ADB=∠AEB=90∘\angle ADB = \angle AEB = 90^\circ.
3. Applying Right-Triangle Congruence (RHS Rule):
   
   • In right-angled triangles ABD and ABE:
     • AD = BE (Given condition)
     • ∠ADB=∠AEB=90∘\angle ADB = \angle AEB = 90^\circ (Right angles)
     • AB = AB (Common hypotenuse)
   • By the RHS Congruence Theorem, triangle ABD \cong triangle ABE.
4. Consequence of Congruence:
   
   • Since the corresponding sides of congruent triangles are equal, we get: BD = EC.
   • This implies that triangle ABC is symmetric about the perpendicular bisector.
5. Conclusion:
   
   • Since two sides of triangle ABC are equal (AB = AC), it follows that ABC is an isosceles triangle.

Summary of Proof in a Table

Here is a table to understand the properties

Step	Explanation
1. Construct Altitudes	Two equal altitudes, AD and BE, are drawn in triangle ABC.
2. Identify Right Angles	∠ADB=∠AEB=90∘\angle ADB = \angle AEB = 90^\circ.
3. Apply RHS Congruence	Right triangles ABD and ABE are congruent.
4. Use Congruence Properties	Corresponding sides are equal: BD = EC.
5. Conclusion	Triangle ABC is isosceles with AB = AC.

Practical Implications of the Result

Understanding this property helps in:

• Triangle classification: If two altitudes are equal, we can immediately identify the triangle as isosceles.
• Problem-solving: This theorem is useful in geometric proofs and constructions.
• Real-life applications: Architectural designs and engineering structures use symmetrical properties of isosceles triangles for stability.

Thus, we have rigorously proved that if two altitudes of a triangle are equal, then the triangle must be isosceles. This proof strengthens our understanding of geometric properties and congruence theorems, making it a valuable concept in mathematics.

Common Doubts

How Many Squares Are There in a Chess Board?

How do you split the middle term in quadratic equations?

Is 0 a rational, irrational, natural, whole, integer or real number?

The instrument in the geometry box in the shape of a triangle is called a